Difference between revisions of "Hodge theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W.V.D. Hodge, "The topological invariants of algebraic varieties" , ''Proc. Internat. Congress Mathematicians (Cambridge, 1950)'' , '''1''' , Amer. Math. Soc. (1952) pp. 182–192 {{MR|0046075}} {{ZBL|0048.41701}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1962) {{MR|1015714}} {{MR|0051571}} {{MR|0003947}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , '''1''' , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) {{MR|}} {{ZBL|0534.58003}} </TD></TR></table> |
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) {{MR|0608414}} {{ZBL|0435.32004}} </TD></TR></table> |
Revision as of 21:53, 30 March 2012
Hodge's index theorem: The index (signature) 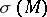 of a compact Kähler manifold
of a compact Kähler manifold 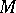 of complex dimension
of complex dimension 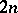 can be computed by the formula
can be computed by the formula
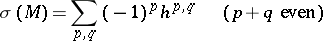 |
where 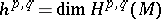 is the dimension of the space of harmonic forms of type
is the dimension of the space of harmonic forms of type  on
on  (cf. Harmonic form). This was proved by W.V.D. Hodge .
(cf. Harmonic form). This was proved by W.V.D. Hodge .
Hodge's theorem on the decomposition of the space of smooth sections of an elliptic complex on a compact manifold into the orthogonal direct sum of subspaces of harmonic exact and co-exact sections (see Laplace operator). This was proved by W.V.D. Hodge [2] for the de Rham complex
 |
on an orientable compact Riemannian manifold  . In this case Hodge's theorem asserts that for any
. In this case Hodge's theorem asserts that for any 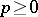 the space
the space 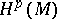 of harmonic forms on
of harmonic forms on 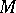 is finite-dimensional and that there exists a unique operator
is finite-dimensional and that there exists a unique operator 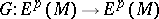 (the Green–de Rham operator) satisfying the conditions
(the Green–de Rham operator) satisfying the conditions
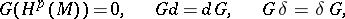 |
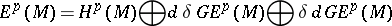 |
(the Hodge decomposition). In particular, 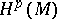 is isomorphic to the real cohomology space
is isomorphic to the real cohomology space 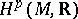 of
of 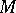 . Another important special case is the Hodge theorem for the Dolbeault complex on a compact complex manifold
. Another important special case is the Hodge theorem for the Dolbeault complex on a compact complex manifold 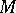 (see Differential form) [3]. These results lead to the classical Hodge structure in the cohomology spaces of a compact Kähler manifold.
(see Differential form) [3]. These results lead to the classical Hodge structure in the cohomology spaces of a compact Kähler manifold.
References
| [1] | W.V.D. Hodge, "The topological invariants of algebraic varieties" , Proc. Internat. Congress Mathematicians (Cambridge, 1950) , 1 , Amer. Math. Soc. (1952) pp. 182–192 MR0046075 Zbl 0048.41701 |
| [2] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1962) MR1015714 MR0051571 MR0003947 |
| [3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1 , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [4] | G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) Zbl 0534.58003 |
Comments
References
| [a1] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) MR0608414 Zbl 0435.32004 |
Hodge theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hodge_theorem&oldid=13225