Hodge theorem
Hodge's index theorem: The index (signature) 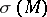 of a compact Kähler manifold
of a compact Kähler manifold 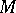 of complex dimension
of complex dimension 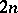 can be computed by the formula
can be computed by the formula
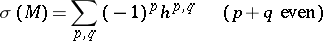 |
where 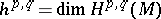 is the dimension of the space of harmonic forms of type
is the dimension of the space of harmonic forms of type 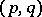 on
on 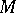 (cf. Harmonic form). This was proved by W.V.D. Hodge .
(cf. Harmonic form). This was proved by W.V.D. Hodge .
Hodge's theorem on the decomposition of the space of smooth sections of an elliptic complex on a compact manifold into the orthogonal direct sum of subspaces of harmonic exact and co-exact sections (see Laplace operator). This was proved by W.V.D. Hodge [2] for the de Rham complex
 |
on an orientable compact Riemannian manifold 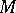 . In this case Hodge's theorem asserts that for any
. In this case Hodge's theorem asserts that for any 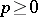 the space
the space 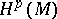 of harmonic forms on
of harmonic forms on 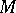 is finite-dimensional and that there exists a unique operator
is finite-dimensional and that there exists a unique operator 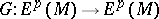 (the Green–de Rham operator) satisfying the conditions
(the Green–de Rham operator) satisfying the conditions
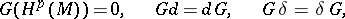 |
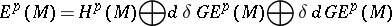 |
(the Hodge decomposition). In particular, 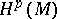 is isomorphic to the real cohomology space
is isomorphic to the real cohomology space 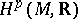 of
of 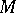 . Another important special case is the Hodge theorem for the Dolbeault complex on a compact complex manifold
. Another important special case is the Hodge theorem for the Dolbeault complex on a compact complex manifold 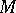 (see Differential form) [3]. These results lead to the classical Hodge structure in the cohomology spaces of a compact Kähler manifold.
(see Differential form) [3]. These results lead to the classical Hodge structure in the cohomology spaces of a compact Kähler manifold.
References
| [1] | W.V.D. Hodge, "The topological invariants of algebraic varieties" , Proc. Internat. Congress Mathematicians (Cambridge, 1950) , 1 , Amer. Math. Soc. (1952) pp. 182–192 |
| [2] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1962) |
| [3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , 1 , Wiley (Interscience) (1978) |
| [4] | G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) |
Comments
References
| [a1] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Hodge theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hodge_theorem&oldid=13225