Difference between revisions of "Von Staudt-Clausen theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Von Staudt–Clausen theorem to Von Staudt-Clausen theorem: ascii title) |
(No difference)
| |
Revision as of 18:54, 24 March 2012
An important result on the arithmetic of the Bernoulli numbers 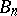 , first published in 1840 by Th. Clausen [a1] without proof, and independently by K.G.C. von Staudt [a2]:
, first published in 1840 by Th. Clausen [a1] without proof, and independently by K.G.C. von Staudt [a2]:
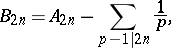 | (a1) |
where 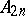 is an integer and the summation is over all prime numbers
is an integer and the summation is over all prime numbers 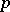 such that
such that 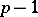 divides
divides 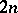 (cf. also Prime number). Since
(cf. also Prime number). Since 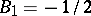 , the identity (a1) holds also for
, the identity (a1) holds also for 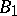 . An immediate consequence of the von Staudt–Clausen theorem is the complete determination of the denominators of the Bernoulli numbers: If
. An immediate consequence of the von Staudt–Clausen theorem is the complete determination of the denominators of the Bernoulli numbers: If 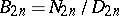 , with
, with  , then
, then
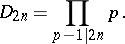 |
The von Staudt–Clausen theorem has been extended in a variety of ways, among them:
1) K.G.C. von Staudt [a3] showed that the integer 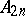 in (a1) has the same parity as the number of primes
in (a1) has the same parity as the number of primes 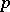 such that
such that 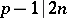 ; M.A. Stern [a4] derived a congruence modulo
; M.A. Stern [a4] derived a congruence modulo 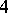 between these two quantities. Ch. Hermite [a5] found a recurrence relation among the
between these two quantities. Ch. Hermite [a5] found a recurrence relation among the 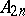 , and R. Lipschitz [a6] derived an asymptotic relation for the
, and R. Lipschitz [a6] derived an asymptotic relation for the 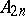 .
.
2) The identity (a1) implies that  if
if 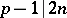 . L. Carlitz [a7] showed that
. L. Carlitz [a7] showed that 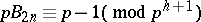 if
if 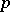 is a prime number and
is a prime number and 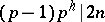 . A different extension modulo higher powers of
. A different extension modulo higher powers of 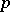 is given in [a8].
is given in [a8].
3) H.S. Vandiver [a9] extended (a1) to Bernoulli polynomials evaluated at rational arguments: Let 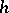 and
and 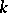 be relatively prime integers. If
be relatively prime integers. If  is even, then
is even, then
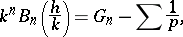 |
where 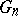 is an integer and the summation is over all prime numbers
is an integer and the summation is over all prime numbers 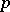 such that
such that 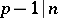 but
but 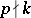 . If
. If  is odd, then
is odd, then 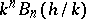 is an integer, except for
is an integer, except for 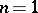 and
and 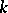 odd, in which case
odd, in which case  . It has also been shown [a10] that for all integers
. It has also been shown [a10] that for all integers 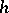 ,
, 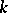 ,
,  with
with 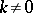 and
and 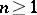 ,
, 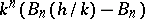 is an integer.
is an integer.
4) Von Staudt [a3] proved a related result on the numerators of the Bernoulli numbers. Combined with (a1), it can be given in the following form: For any integer 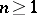 , the denominator of
, the denominator of 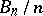 is
is
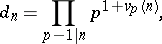 |
where the product is over all prime numbers 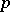 such that
such that 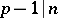 , and
, and 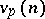 denotes the highest power of
denotes the highest power of 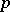 dividing
dividing  .
.
5) R. Rado [a11] showed that, given a positive integer  , there exist infinitely many Bernoulli numbers
, there exist infinitely many Bernoulli numbers 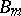 such that
such that  is an integer.
is an integer.
Numerous results on Bernoulli and allied numbers rely on the von Staudt–Clausen theorem. An early application was the explicit evaluation of Bernoulli numbers; more recent applications lie, for instance, in the theory of 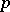 -adic
-adic 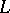 -functions; see [a12], p. 56.
-functions; see [a12], p. 56.
The von Staudt–Clausen theorem has been generalized in various directions. In particular, analogues of the theorem exist for most concepts of generalized Bernoulli numbers, among them the generalized Bernoulli numbers associated with Dirichlet characters (see, e.g., [a13]), degenerate Bernoulli numbers [a14], periodic Bernoulli numbers (or cotangent numbers) [a15], Bernoulli–Carlitz numbers [a16], Bernoulli–Hurwitz numbers [a17], and others. Another vast generalization was given by F. Clarke [a18].
References
| [a1] | Th. Clausen, "Lehrsatz aus einer Abhandlung über die Bernoullischen Zahlen" Astr. Nachr. , 17 (1840) pp. 351–352 |
| [a2] | K.G.C. von Staudt, "Beweis eines Lehrsatzes die Bernoulli'schen Zahlen betreffend" J. Reine Angew. Math. , 21 (1840) pp. 372–374 |
| [a3] | K.G.C. von Staudt, "De Numeris Bernoullianis" , Erlangen (1845) |
| [a4] | M.A. Stern, "Über eine Eigenschaft der Bernoulli'schen Zahlen" J. Reine Angew. Math. , 81 (1876) pp. 290–294 |
| [a5] | Ch. Hermite, "Extrait d'une lettre à M. Borchardt (sur les nombres de Bernoulli)" J. Reine Angew. Math. , 81 (1876) pp. 93–95 |
| [a6] | R. Lipschitz, "Sur la représentation asymptotique de la valeur numérique ou de la partie entière des nombres de Bernoulli" Bull. Sci. Math. (2) , 10 (1886) pp. 135–144 |
| [a7] | L. Carlitz, "A note on the Staudt–Clausen theorem" Amer. Math. Monthly , 64 (1957) pp. 19–21 |
| [a8] | Zhi-Hong Sun, "Congruences for Bernoulli numbers and Bernoulli polynomials" Discrete Math. , 163 (1997) pp. 153–163 |
| [a9] | H.S. Vandiver, "Simple explicit expressions for generalized Bernoulli numbers of the first order" Duke Math. J. , 8 (1941) pp. 575–584 |
| [a10] | F. Clarke, I.Sh. Slavutskii, "The integrality of the values of Bernoulli polynomials and of generalised Bernoulli numbers" Bull. London Math. Soc. , 29 (1997) pp. 22–24 |
| [a11] | R. Rado, "A note on Bernoullian numbers" J. London Math. Soc. , 9 (1934) pp. 88–90 |
| [a12] | L.C. Washington, "Introduction to cyclotomic fields" , Springer (1982) (Second ed.: 1996) |
| [a13] | L. Carlitz, "Arithmetic properties of generalized Bernoulli numbers" J. Reine Angew. Math. , 202 (1959) pp. 174–182 |
| [a14] | L. Carlitz, "A degenerate Staudt–Clausen theorem" Arch. Math. Phys. , 7 (1956) pp. 28–33 |
| [a15] | K. Girstmair, "Ein v. Staudt–Clausenscher Satz für periodische Bernoulli–Zahlen" Monatsh. Math. , 104 (1987) pp. 109–118 |
| [a16] | D. Goss, "Von Staudt for 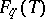 " Duke Math. J. , 45 (1978) pp. 887–910 " Duke Math. J. , 45 (1978) pp. 887–910 |
| [a17] | N. Katz, "The congruences of Clausen–von Staudt and Kummer for Bernoulli–Hurwitz numbers" Math. Ann. , 216 (1975) pp. 1–4 |
| [a18] | F. Clarke, "The universal von Staudt theorems" Trans. Amer. Math. Soc. , 315 (1989) pp. 591–603 |
Von Staudt-Clausen theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Von_Staudt-Clausen_theorem&oldid=18280