Skolem-Noether theorem

In its classical form, the Skolem–Noether theorem can be stated as follows. Let 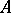and 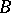be finite-dimensional algebras over a field 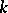, and assume that 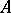is simple and 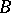is central simple (cf. also Simple algebra; Central algebra; Field). If 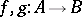are 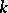-algebra homomorphisms, then there exists an invertible 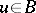such that

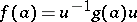for all 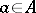. A proof can be found, for example, in [a5], p. 21, or [a4], Chap, 4. In particular, every 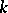-algebra automorphism of a central simple algebra is inner (cf. also Inner automorphism). This can be generalized to an Azumaya algebra 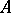over a commutative ring 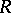(cf. also Separable algebra): There is an exact sequence, usually called the Rosenberg–Zelinsky exact sequence:

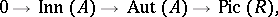where 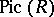is the Picard group of 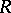, is the group of 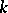-algebra automorphisms of 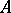and 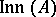is the subgroup consisting of inner automorphisms. The proof is an immediate application of the categorical characterization of Azumaya algebras: An 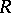-algebra 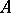is Azumaya if and only if the categories of -modules and 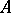-bimodules are equivalent via the functors sending an 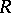-module 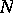to 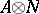, and sending an 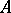-bimodule 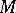to

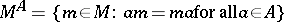(see, e.g., [a6], IV.1, for details).

The Skolem–Noether theorem plays a crucial role in the theory of the Brauer group; for example, it is used in the proof of the Hilbert 90 theorem (cf. also Hilbert theorem) and the cross product theorem. There exist versions of the Skolem–Noether theorem (and the Rosenberg–Zelinsky exact sequence) for other generalized types of Azumaya algebras; in particular, for Azumaya algebras over schemes [a3], Azumaya algebras relative to a torsion theory [a7], III.3.26, and Long's 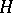-dimodule Azumaya algebras [a1], [a2].

References

[a1]	M. Beattie, "Automorphisms of 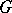-Azumaya algebras" Canad. J. Math. , 37 (1985) pp. 1047–1058
[a2]	S. Caenepeel, "Brauer groups, Hopf algebras and Galois theory" , K-Monographs Math. , 4 , Kluwer Acad. Publ. (1998)
[a3]	A. Grothendieck, "Le groupe de Brauer I" , Dix Exposés sur la cohomologie des schémas , North-Holland (1968)
[a4]	I.N. Herstein, "Noncommutative rings" , Carus Math. Monographs , 15 , Math. Assoc. Amer. (1968)
[a5]	I. Kersten, "Brauergruppen von Körpern" , Aspekte der Math. , D6 , Vieweg (1990)
[a6]	M.A. Knus, M. Ojanguren, "Théorie de la descente et algèbres d'Azumaya" , Lecture Notes in Mathematics , 389 , Springer (1974)
[a7]	F. Van Oystaeyen, A. Verschoren, "Relative invariants of rings I" , Monographs and Textbooks in Pure and Appl. Math. , 79 , M. Dekker (1983)