Difference between revisions of "Painlevé equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Painlevé equation to Painleve equation: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
The common name for a group of six special ordinary differential equations of the type
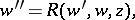 |
where 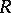 is a rational function in
is a rational function in 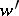 and
and 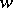 and an analytic function in
and an analytic function in  . Any such equation having only fixed singular points (cf. Movable singular point) can be reduced to one out of 50 canonical equations. These include linear equations, Riccati equations (cf. Riccati equation) and other well-known equations, as well as the six other equations known as the Painlevé equations, and having solutions in the form of transcendental Painlevé functions, which are special functions that do not reduce to other known ones. Arranged in the generally-accepted order, the Painlevé equations have the following form (
. Any such equation having only fixed singular points (cf. Movable singular point) can be reduced to one out of 50 canonical equations. These include linear equations, Riccati equations (cf. Riccati equation) and other well-known equations, as well as the six other equations known as the Painlevé equations, and having solutions in the form of transcendental Painlevé functions, which are special functions that do not reduce to other known ones. Arranged in the generally-accepted order, the Painlevé equations have the following form ( are constants):
are constants):
1) 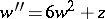 ;
;
2)  ;
;
3) 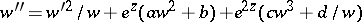 ,
, 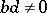 ;
;
4) 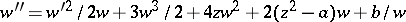 ;
;
5) 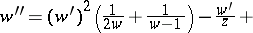
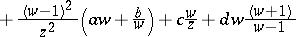 ;
;
6) 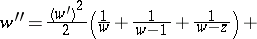
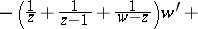
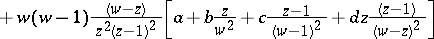 .
.
These results were first obtained in researches by P. Painlevé [1], [2]. These were continued, refined and supplemented by B. Gambier [3].
References
| [1] | P. Painlevé, "Mémoire sur les équations différentielles dont l'intégrale générale est uniforme" Bull. Soc. Math. France , 28 (1900) pp. 201–261 |
| [2] | P. Painlevé, "Sur les équations différentielles du second ordre et d'ordre supérieure dont l'intégrale générale est uniforme" Acta Math. , 25 (1902) pp. 1–85 |
| [3] | B. Gambier, "Sur les équations différentielles du second ordre et du premier degré dont l'intégrale générale est à points critiques fixes" Acta Math. , 33 (1910) pp. 1–55 |
| [4] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
| [5] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
Comments
The Painlevé equations and the Painlevé property (absence of movable singular points) play an important role in the theory of completely-integrable systems (cf. Soliton). Indeed, the Painlevé property has been proposed as a test for complete integrability. For a survey of the current status of these ideas cf. [a3].
References
| [a1] | M.J. Ablowitz, H. Segur, "Solitons and the inverse scattering transform" , SIAM (1981) |
| [a2] | R.K. Dodd, J.C. Eilbeck, J.D. Gibbon, H.C. Morris, "Solitons and nonlinear wave equations" , Acad. Press (1982) |
| [a3] | H. Yoshida, B. Grammaticos, A. Ramani, "Painlevé resonances versus Kowalevski exponents: some exact results on singularity structure and integrability of dynamical systems" Acta Appl. Math. , 8 (1987) pp. 75–104 |
| [a4] | R. Gérard (ed.) G. Reeb (ed.) A. Sec (ed.) , Oeuvres de P. Painlevé , CNRS (1972–1975) |
| [a5] | E. Hille, "Lectures on ordinary differential equations" , Addison-Wesley (1969) |
Painlevé equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Painlev%C3%A9_equation&oldid=17908