Keldysh-Lavrent'ev example

An example of a simply-connected domain 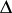in the complex -plane bounded by a rectifiable Jordan curve but not belonging to the class 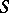of Smirnov domains (cf. Smirnov domain).

Let 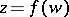be a function realizing a conformal mapping of the unit disc 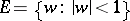onto a simply-connected domain 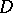bounded by a rectifiable Jordan curve. It is known that 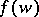is continuous and one-to-one in the closed disc 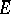and that the logarithm of the modulus of the derivative 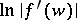can be represented in 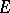by the Poisson–Stieltjes integral

(*)

where is the normalized Borel measure on , 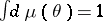. The class 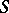consists of those closed domains 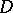for which the measure 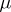in the representation (*) is absolutely continuous with respect to the Lebesgue measure on 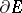and the integral (*) becomes the Poisson–Lebesgue integral (cf. Poisson integral) of the boundary values , which exist almost-everywhere on .

M.V. Keldysh and M.A. Lavrent'ev [1] constructed for any 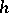, , 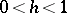a simply-connected domain 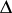bounded by a rectifiable Jordan curve 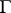, located in the disc 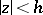, , 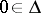such that under a conformal mapping of 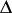onto ,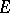

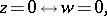and the image of any arc 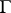on the circle 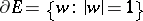is an arc of the same length. This domain 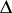does not belong to the class 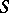, since 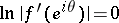almost-everywhere on .

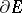A complete solution of the problem of characterizing domains of class 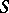(domains of Smirnov type) has so far (1989) not been obtained (see [2], [3]).

References

[1]	M.V. Keldysh, M.A. Lavrent'ev, "Sur la répresentation conforme des domains limités par des courbes rectifiables" Ann. Ecole Norm. Sup. , 54 (1937) pp. 1–38
[2]	I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[3]	A.J. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. i Tekhn. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian)

Comments

The construction of Keldysh and Lavrent'ev is extraordinarily complicated. For a more accessible treatment, see [a1] and [a2].

References

[a1]	P.L. Duren, H.S. Shapiro, A.L. Shields, "Singular measures and domains not of Smirnov type" Duke Math. J. , 33 (1966) pp. 247–254
[a2]	G. Piranian, "Two monotonic, singular, uniformly almost smooth functions" Duke Math. J. , 33 (1966) pp. 254–262