Difference between revisions of "Kac-Moody algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Kac–Moody algebra to Kac-Moody algebra: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
Kac–Moody Lie algebra
Let 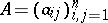 be an
be an 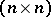 -matrix satisfying conditions (see Cartan matrix)
-matrix satisfying conditions (see Cartan matrix)
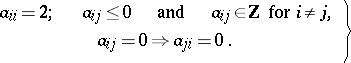 | (a1) |
The associated Kac–Moody algebra 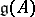 is a Lie algebra over
is a Lie algebra over 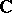 on
on 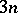 generators
generators 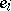 ,
, 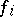 ,
, 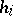 (called the Chevalley generators) and the following defining relations:
(called the Chevalley generators) and the following defining relations:
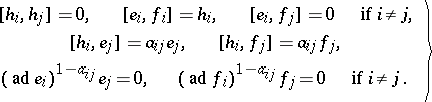 | (a2) |
The Lie algebra 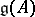 is finite dimensional if and only if the matrix
is finite dimensional if and only if the matrix 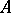 is positive definite (i.e. all principal minors of
is positive definite (i.e. all principal minors of 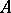 are positive, cf. also Minor). One gets in this way all finite-dimensional semi-simple Lie algebras over
are positive, cf. also Minor). One gets in this way all finite-dimensional semi-simple Lie algebras over 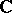 (see Lie algebra, semi-simple). Thus, Kac–Moody algebras are infinite-dimensional analogues of the finite-dimensional semi-simple Lie algebras.
(see Lie algebra, semi-simple). Thus, Kac–Moody algebras are infinite-dimensional analogues of the finite-dimensional semi-simple Lie algebras.
A systematic study of Kac–Moody algebras was started independently by V.G. Kac [a1] and R.V. Moody [a2], and subsequently many results of the theory of finite-dimensional semi-simple Lie algebras have been carried over to Kac–Moody algebras. The main technical tool of the theory is the generalized Casimir operator (cf. Casimir element), which can be constructed provided that the matrix 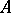 is symmetrizable, i.e.
is symmetrizable, i.e. 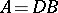 for some invertible diagonal matrix
for some invertible diagonal matrix 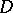 and symmetric matrix
and symmetric matrix 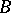 [a3]. In the non-symmetrizable case more sophisticated geometric methods are required [a4], [a5].
[a3]. In the non-symmetrizable case more sophisticated geometric methods are required [a4], [a5].
One of the most important ingredients of the theory of Kac–Moody algebras are integrable highest-weight representations (cf. also Representation with a highest weight vector). Given an  -tuple of non-negative integers
-tuple of non-negative integers 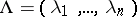 , the integrable highest-weight representation
, the integrable highest-weight representation 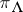 of a Kac–Moody algebra
of a Kac–Moody algebra 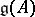 is its irreducible representation on a complex vector space
is its irreducible representation on a complex vector space 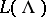 , which is determined by the property that there exists a non-zero vector
, which is determined by the property that there exists a non-zero vector 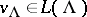 such that
such that
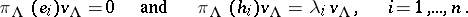 |
Note that 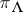 are precisely all irreducible finite-dimensional representations of a finite-dimensional Kac–Moody algebra
are precisely all irreducible finite-dimensional representations of a finite-dimensional Kac–Moody algebra 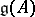 .
.
The basic result of the theory of integrable highest-weight representations is the Weyl–Kac character formula [a3], which gives an explicit expression for the formal power series 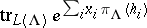 in the
in the 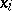 in terms of
in terms of 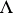 (see also Character formula).
(see also Character formula).
The numerous applications of Kac–Moody algebras are mainly related to the fact that the Kac–Moody algebras associated to positive semi-definite indecomposable Cartan matrices (called affine matrices) admit a very explicit construction. (A matrix is called indecomposable if it does not become block-diagonal after arbitrary permutation of the index set.) These Kac–Moody algebras are called affine algebras.
Below a construction of "non-twisted" affine algebras is given. Let 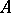 be a positive-definite indecomposable Cartan matrix and let
be a positive-definite indecomposable Cartan matrix and let 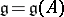 be the associated simple finite-dimensional Lie algebra with Chevalley generators
be the associated simple finite-dimensional Lie algebra with Chevalley generators 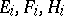 ,
, 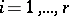 . There exists a unique (up to a constant multiple) non-zero element
. There exists a unique (up to a constant multiple) non-zero element 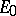 (respectively,
(respectively, 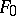 ) in
) in 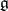 such that
such that 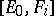 (respectively,
(respectively, 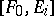 ) vanishes for
) vanishes for 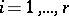 . Then
. Then 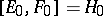 , a linear combination of the
, a linear combination of the 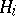 (
(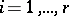 ), and one normalizes
), and one normalizes 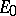 and
and 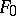 by the conditions
by the conditions 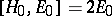 ,
, 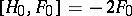 . Then:
. Then: 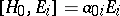 ,
, 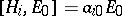 for
for 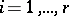 , where the
, where the 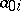 are certain non-positive integers, and one puts
are certain non-positive integers, and one puts
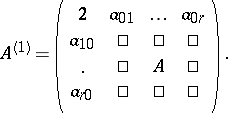 |
This is a positive semi-definite 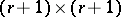 matrix satisfying (a1) (called the extended Cartan matrix of
matrix satisfying (a1) (called the extended Cartan matrix of 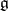 ). These matrices, along with all affine matrices, are listed in Lie algebra, graded. The associated affine algebra
). These matrices, along with all affine matrices, are listed in Lie algebra, graded. The associated affine algebra
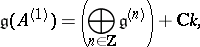 |
where 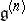 is the
is the  -th copy of
-th copy of 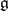 and
and 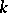 is a central element (i.e.
is a central element (i.e. 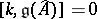 ), with the following commutation relations:
), with the following commutation relations:
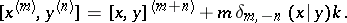 |
Here 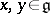 ,
, 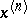 denotes the element
denotes the element  taken from
taken from 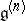 and
and 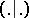 is the Killing form on
is the Killing form on 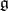 normalized by the condition
normalized by the condition 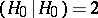 . (Note that for
. (Note that for 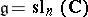 , one has
, one has 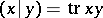 .) The canonical generators of
.) The canonical generators of 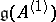 are:
are:
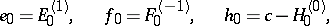 |
 |
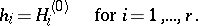 |
In more geometric terms, 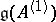 is a central extension (by
is a central extension (by 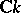 ) of the loop algebra, i.e. the Lie algebra of regular mappings of
) of the loop algebra, i.e. the Lie algebra of regular mappings of 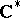 to
to 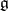 :
:
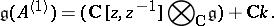 |
This observation leads to geometric applications of affine algebras and the corresponding groups, called the loop groups (see [a6]).
In an integrable highest-weight representation 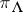 , the central element
, the central element 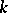 acts as a non-negative integral scalar, also denoted by
acts as a non-negative integral scalar, also denoted by 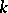 , which is called the level of
, which is called the level of 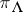 . The only
. The only 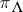 of level
of level  is the trivial representation. A remarkable feature of the representation theory of the affine algebras is the existence of explicit canonical constructions for the
is the trivial representation. A remarkable feature of the representation theory of the affine algebras is the existence of explicit canonical constructions for the 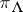 of level
of level 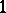 . Below the simplest "vertex operator" construction for the basic representation
. Below the simplest "vertex operator" construction for the basic representation 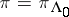 , where
, where 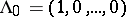 , is explained. It uses the vertex operators, which are defined as follows. Let
, is explained. It uses the vertex operators, which are defined as follows. Let 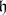 be an
be an  -dimensional complex vector space with a symmetric bilinear form
-dimensional complex vector space with a symmetric bilinear form 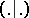 and let
and let 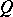 be a lattice in
be a lattice in 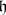 of rank
of rank  . For each
. For each 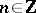 , take a copy
, take a copy 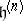 of
of 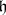 and let
and let 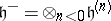 . Let
. Let 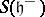 be the symmetric algebra over
be the symmetric algebra over 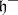 and let
and let 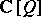 be the group algebra of
be the group algebra of 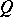 with the inclusion
with the inclusion 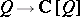 denoted by
denoted by 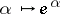 . Consider the complex commutative associative algebra
. Consider the complex commutative associative algebra
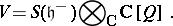 |
For 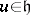 and
and 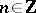 define an operator
define an operator 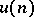 on
on 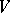 as follows. For
as follows. For 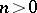 ,
, 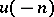 is the operator of multiplication by
is the operator of multiplication by 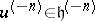 ; for
; for 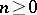 ,
, 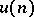 is the derivation of
is the derivation of 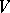 defined by:
defined by:
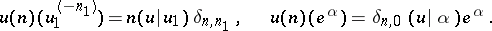 |
For 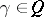 such that
such that 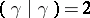 , define the vertex operator
, define the vertex operator
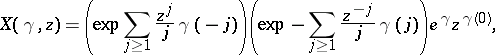 |
where 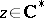 . Expanding in powers of
. Expanding in powers of  :
: 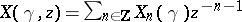 , one obtains a sequence of operators
, one obtains a sequence of operators 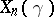 on
on 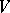 . Let now
. Let now 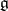 be a simple Lie algebra with the Cartan matrix
be a simple Lie algebra with the Cartan matrix 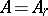 ,
, 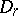 or
or 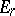 , choose a Cartan subalgebra
, choose a Cartan subalgebra 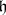 of
of 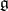 , let
, let 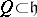 be the root lattice (identifying
be the root lattice (identifying 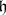 with
with 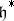 using the form
using the form 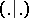 ), and let
), and let 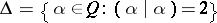 be the root system of
be the root system of 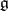 . Choose a bimultiplicative function
. Choose a bimultiplicative function 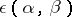 on
on 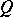 with values
with values 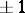 such that
such that 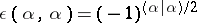 . For
. For 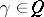 , define an operator
, define an operator 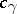 on
on 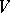 by
by 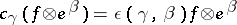 . Then
. Then 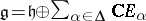 with commutation relations:
with commutation relations:
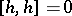 ;
; 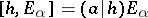 for
for 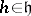 ;
;
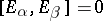 if
if 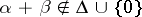 ;
;
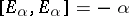 ;
; 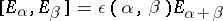 if
if 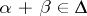 .
.
The basic representation of 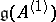 is then defined on
is then defined on 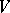 by the following formulas [a11]:
by the following formulas [a11]:
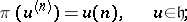 |
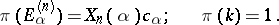 |
This is called the homogeneous vertex operator construction of the basic representation.
The vertex operators were introduced in string theory around 1969, but the vertex operator construction entered string theory only at its revival in the mid 1980s. Thus, the representation theory of affine algebras became an important ingredient of string theory (see [a12]).
The vertex operators turned out to be useful even in the theory of finite simple groups. Namely, a twist of the homogeneous vertex operator construction based on the Leech lattice produced the 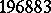 -dimensional Griess algebra and its automorphism group, the famous finite simple Monster group (see Sporadic simple group) [a13].
-dimensional Griess algebra and its automorphism group, the famous finite simple Monster group (see Sporadic simple group) [a13].
The vertex operator constructions were, quite unexpectedly, applied to the theory of soliton equations. This was based on the observation (see [a14]) that the orbit of the vector 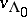 of the basic representation under the loop group satisfies an infinite hierarchy of partial differential equations, the simplest of them being classical soliton equations, like the Korteweg–de Vries equation.
of the basic representation under the loop group satisfies an infinite hierarchy of partial differential equations, the simplest of them being classical soliton equations, like the Korteweg–de Vries equation.
The link of the representation theory of affine algebras to the conformal field theory is given by the Sugawara construction. Let 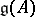 be a simple finite-dimensional algebra and let
be a simple finite-dimensional algebra and let 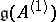 be the corresponding affine algebra. Choose bases
be the corresponding affine algebra. Choose bases 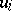 and
and 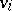 of
of 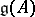 such that
such that 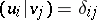 . Let
. Let
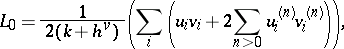 |
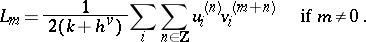 |
Here 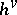 is the dual Coxeter number (defined by: Killing form
is the dual Coxeter number (defined by: Killing form 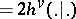 ). Then one has
). Then one has
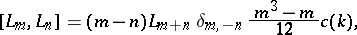 |
where
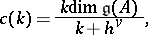 |
producing thereby a representation of the Virasoro algebra.
The character of an integrable highest-weight representation 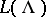 of level
of level 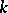 of an affine algebra, multiplied by a suitable power of
of an affine algebra, multiplied by a suitable power of 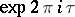 , can be written in the following form:
, can be written in the following form:
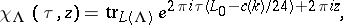 |
where 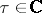 and
and 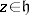 . This is a series which converges for
. This is a series which converges for 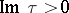 to a modular function. Moreover, the linear span of the functions
to a modular function. Moreover, the linear span of the functions 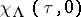 for
for 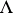 of fixed level
of fixed level 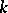 is invariant under the modular transformations
is invariant under the modular transformations
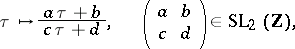 |
and the matrix 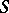 of the transformation
of the transformation 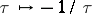 is known explicitly [a7]. For example, in the case
is known explicitly [a7]. For example, in the case 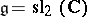 ,
,
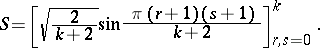 |
This turned out to be a key fact in the representation theory of affine algebras, as well as its applications to conformal field theory (see [a8]), to  -dimensional lattice models [a9], and even to knot theory [a10].
-dimensional lattice models [a9], and even to knot theory [a10].
References
| [a1] | V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" Math. USSR Izv. , 2 (1968) pp. 1271–1311 Izv. Akad. Nauk USSR Ser. Mat. , 32 (1968) pp. 1923–1967 |
| [a2] | R.V. Moody, "A new class of Lie algebras" J. of Algebra , 10 (1968) pp. 211–230 |
| [a3] | V.G. Kac, "Infinite-dimensional Lie algebras and Dedekind's 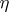 -function" Funct. Anal. Appl. , 8 (1974) pp. 68–70 Funkts. Anal. i Prilozhen. , 8 : 1 (1974) pp. 77–78 -function" Funct. Anal. Appl. , 8 (1974) pp. 68–70 Funkts. Anal. i Prilozhen. , 8 : 1 (1974) pp. 77–78 |
| [a4] | S. Kumar, "Demazure character formula in arbitrary Kac–Moody setting" Invent. Math. , 89 (1987) pp. 395–423 |
| [a5] | O. Mathieu, "Formules de caractères pour les algèbres de Kac–Moody générales" Astérisque , 159–160 (1988) pp. 1–266 |
| [a6] | A. Pressley, G. Segal, "Loop groups" , Oxford Univ. Press (1986) |
| [a7] | V.G. Kac, D.H. Peterson, "Infinite-dimensional Lie algebras, theta functions and modular forms" Adv. in Math. , 53 (1984) pp. 125–264 |
| [a8] | E. Verlinde, "Fusion rules and modular transformations in 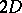 conformal field theory" Nucl. Phys. , B300 pp. 360–375 conformal field theory" Nucl. Phys. , B300 pp. 360–375 |
| [a9] | E. Date, M. Jimbo, A. Kuniba, T. Miwa, M. Okado, "Exactly solvable SOS models" Nucl. Phys. , B290 (1987) pp. 231–273 |
| [a10] | C.N. Yang (ed.) M.L. Ge (ed.) , Braid group, knot theory and statistical mechanics , World Sci. (1989) |
| [a11] | I.B. Frenkel, V.G. Kac, "Basic representations of affine Lie algebras and dual resonance models" Invent. Math. , 62 (1980) pp. 23–66 |
| [a12] | M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , Cambridge Univ. Press (1987) |
| [a13] | I. Frenkel, J. Lepowsky, A. Meurman, "Vertex operator algebras and the Monster" , Acad. Press (1989) |
| [a14] | E. Date, M. Jimbo, M. Kashiwara, T. Miwa, "Transformation groups for soliton equations" M. Jimbo (ed.) T. Miwa (ed.) , Proc. RIMS Symp. , World Sci. (1983) pp. 39–120 |
| [a15] | V.G. Kac, "Infinite-dimensional Lie algebras" , Cambridge Univ. Press (1985) |
| [a16] | V.G. Kac, A.K. Raina, "Bombay lectures on highest weight representations" , World Sci. (1987) |
Kac-Moody algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kac-Moody_algebra&oldid=19027