Difference between revisions of "Anisotropic kernel"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Tits, "Classification of algebraic simple groups" , ''Algebraic Groups and Discontinuous Subgroups'' , ''Proc. Symp. Pure Math.'' , '''9''' , Amer. Math. Soc. (1966) pp. 33–62 | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Tits, "Classification of algebraic simple groups" , ''Algebraic Groups and Discontinuous Subgroups'' , ''Proc. Symp. Pure Math.'' , '''9''' , Amer. Math. Soc. (1966) pp. 33–62 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Borel, J. Tits, "Groupes réductifs" ''Publ. Math. IHES'' , '''27''' (1965) pp. 55–150 {{MR|0207712}} {{ZBL|0145.17402}} </TD></TR></table> |
Revision as of 10:19, 24 March 2012
The subgroup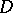 
of a semi-simple algebraic group 
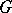, defined over a field 
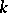, which is the commutator subgroup of the centralizer of a maximal 
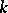-split torus 
; 
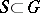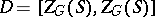. The anisotropic kernel 
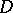is a semi-simple anisotropic group defined over 
; 
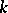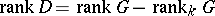. The concept of the anisotropic kernel plays an important role in the study of the 
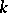-structure of 
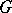[1]. If 
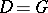, i.e. if 
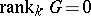, then 
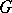is anisotropic over 
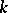; if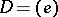 
, the group 
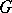is called quasi-split over 
.
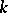References
| [1] | J. Tits, "Classification of algebraic simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62 |
| [2] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 MR0207712 Zbl 0145.17402 |
How to Cite This Entry:
Anisotropic kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anisotropic_kernel&oldid=21814
Anisotropic kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anisotropic_kernel&oldid=21814
This article was adapted from an original article by V.P. Platonov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article