Difference between revisions of "Discrete distribution"
(MSC|60E05 Category:Distribution theory) |
({{MSC|60E05}} Category:Distribution theory (again)) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60E05}} | ||
| + | [[Category:Distribution theory]] | ||
| + | |||
| + | A probability distribution (concentrated) on a finite or countably infinite set of points of a [[Sampling space|sampling space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330601.png" />. More exactly, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330602.png" /> be the sample points and let | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330603.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | ||
| + | |||
| + | be numbers satisfying the conditions | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330604.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | ||
| + | |||
| + | Relations (1) and (2) fully define a discrete distribution on the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330605.png" />, since the probability measure of any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330606.png" /> is defined by the equation | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330607.png" /></td> </tr></table> | ||
| + | |||
| + | Accordingly, the distribution of a random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330608.png" /> is said to be discrete if it assumes, with probability one, a finite or a countably infinite number of distinct values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d0330609.png" /> with probabilities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306010.png" />. In the case of a distribution on the real line, the distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306011.png" /> has jumps at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306012.png" /> equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306013.png" />, and is constant in the intervals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306014.png" />. The following discrete distributions occur most frequently: the [[Binomial distribution|binomial distribution]], the [[Geometric distribution|geometric distribution]], the [[Hypergeometric distribution|hypergeometric distribution]], the [[Negative binomial distribution|negative binomial distribution]], the [[Multinomial distribution|multinomial distribution]], and the [[Poisson distribution|Poisson distribution]]. | ||
| + | |||
| + | |||
| + | |||
| + | ====Comments==== | ||
| + | A word of caution. In the Russian literature, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306015.png" />, whereas in Western literature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d033/d033060/d03306016.png" />. So the distribution functions are slightly different: left continuous in the Russian literature, and right continuous in the Western literature. | ||
Revision as of 17:21, 8 February 2012
2020 Mathematics Subject Classification: Primary: 60E05 [MSN][ZBL]
A probability distribution (concentrated) on a finite or countably infinite set of points of a sampling space 
. More exactly, let 
be the sample points and let
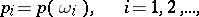 | (1) |
be numbers satisfying the conditions
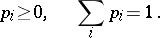 | (2) |
Relations (1) and (2) fully define a discrete distribution on the space 
, since the probability measure of any set 
is defined by the equation
 |
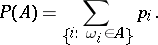Accordingly, the distribution of a random variable 
is said to be discrete if it assumes, with probability one, a finite or a countably infinite number of distinct values 
with probabilities 
. In the case of a distribution on the real line, the distribution function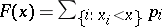 
has jumps at the points 
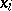equal to 
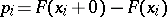, and is constant in the intervals 
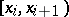. The following discrete distributions occur most frequently: the binomial distribution, the geometric distribution, the hypergeometric distribution, the negative binomial distribution, the multinomial distribution, and the Poisson distribution.
Comments
A word of caution. In the Russian literature,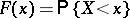 
, whereas in Western literature 
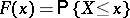. So the distribution functions are slightly different: left continuous in the Russian literature, and right continuous in the Western literature.
Discrete distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discrete_distribution&oldid=20903