Difference between revisions of "Contraction(2)"
From Encyclopedia of Mathematics
(Importing text file) |
m (removed image) |
||
| Line 1: | Line 1: | ||
| − | An affine transformation of the plane under which each point is shifted towards the | + | An affine transformation of the plane under which each point is shifted towards the x-axis, parallel to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025820/c0258202.png" />-axis, by a distance proportional to its ordinate. In a Cartesian coordinate system a contraction is given by the relations |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025820/c0258203.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025820/c0258203.png" /></td> </tr></table> | ||
Revision as of 22:05, 27 March 2011
An affine transformation of the plane under which each point is shifted towards the x-axis, parallel to the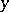 
-axis, by a distance proportional to its ordinate. In a Cartesian coordinate system a contraction is given by the relations
 |
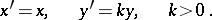A contraction of space towards the 
-plane, parallel to the 
-axis, is given by the relations
 |
Comments
More usually, a contraction is defined as a transformation of a metric space that reduces distances. The notion defined above has no established name in Western literature, but is sometimes called a compression or compression-expansion.
How to Cite This Entry:
Contraction(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction(2)&oldid=15206
Contraction(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contraction(2)&oldid=15206
This article was adapted from an original article by N.V. Reveryuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article