Arithmetic series

of order $m$

The sequence of values of a polynomial of degree $m$:

$$p(x)=a_0+a_1x+\dotsb+a_mx^m,$$

assumed by the polynomial when the variable $x$ takes successive integral non-negative values $x=0,1,\dotsc$. If $m=1$, i.e. $p(x)=a_0+a_1x$, one obtains an arithmetic progression with initial term $a_0$ and difference $a_1$. If $p(x)=x^2$ or $p(x)=x^3$, one obtains sequences of squares or cubes of integers, i.e. special cases of arithmetic series of the second and third orders. If a first difference series is created, constituted by the differences between successive terms of an arithmetic series, then a series of differences of the first difference series (second differences) is written, and then the second differences are used to form third differences, etc., one finds, at the $m$-th stage, that all $m$-th differences are equal. Conversely, if the $m$-th differences of a numerical sequence are all equal, the sequence is an arithmetic series of order $m$. Using this property, it is possible to construct arithmetic series of different orders from their differences. For example, the sequence $1,1,1,\dotsc,$ may be regarded as the first differences of the series of natural numbers $1,2,3,\dotsc$; as the second differences of the series of triangular numbers $1,3,6,10,\dotsc$; as the third differences of the sequence of tetrahedral numbers $1,4,10,20,\dotsc,$ etc. These numbers are so called because triangular numbers represent numbers arranged in the form of a triangle (Fig. a), while tetrahedral numbers represent numbers arranged in the form of tetrahedra (pyramids) (Fig. b).

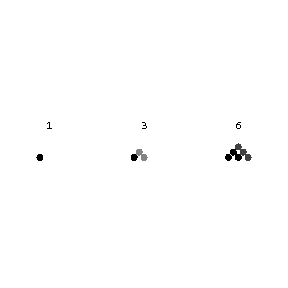
Figure: a013370a

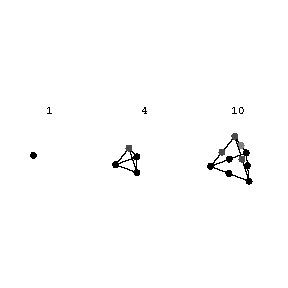
Figure: a013370b

Triangular numbers are expressed by the formula $[n(n+1)]/2$, while tetrahedral numbers are given by the formula

$$\frac{n(n+1)(n+2)}{6},\quad n=1,2,\dotsc.$$

A generalization of triangular numbers is constituted by $k$-gonal or figurate numbers, which played an important role in the development of arithmetic in its various stages.

Figure: a013370c

Figure: a013370d

$k$-gonal numbers are given by the formula:

$$n+(k-2)\frac{n(n-1)}{2},\quad n=1,2,\dotsc.$$

They form an arithmetic series of the second order, with one as their first term, $k$ as their second term and $k-2$ as their second differences. If $k=3$, triangular numbers are obtained; if $k=4$, one obtains squares ($n^2$); if $k=5$, one obtains pentagonal numbers $(3n^2-n)/2$, etc. These appellations will become clear from Fig. c and Fig. d, in which the number of beads arranged in the form of a square or a pentagon is expressed by the respective square or pentagonal number. Figurate numbers satisfy the following theorem, proposed by P. Fermat and first proved by A.L. Cauchy: Any natural number can be represented as a sum of not more than $k$ $k$-gonal numbers.

References

[1]	B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German)
[2]	V.I. Arnol'd, "Theoretical arithmetics" , Moscow (1939) (In Russian)

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️