Meromorphic function
of one complex variable in a domain 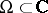 (or on a Riemann surface
(or on a Riemann surface  )
)
A holomorphic function in a domain 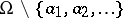 which has at every singular point
which has at every singular point 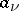 a pole (cf. Pole (of a function), i.e.
a pole (cf. Pole (of a function), i.e. 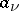 is an isolated point of the set
is an isolated point of the set 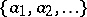 , which has no limit points in
, which has no limit points in  , and
, and 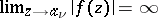 ). The collection
). The collection 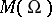 of all meromorphic functions in
of all meromorphic functions in  is a field with respect to the usual pointwise operations followed by redefinition at the removable singularities.
is a field with respect to the usual pointwise operations followed by redefinition at the removable singularities.
The quotient 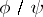 of two arbitrary holomorphic functions in
of two arbitrary holomorphic functions in  ,
, 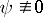 , is a meromorphic function in
, is a meromorphic function in  . Conversely, every meromorphic function in a domain
. Conversely, every meromorphic function in a domain 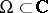 (or on a non-compact Riemann surface
(or on a non-compact Riemann surface  ) can be expressed as
) can be expressed as 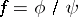 ,
, 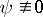 , where
, where 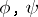 are holomorphic and have no common zeros in
are holomorphic and have no common zeros in  . It follows that on a non-compact Riemann surface
. It follows that on a non-compact Riemann surface  the field
the field 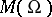 coincides with the field of fractions of the ring
coincides with the field of fractions of the ring 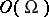 of holomorphic functions in
of holomorphic functions in  .
.
Every meromorphic function 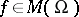 defines a continuous mapping
defines a continuous mapping 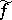 of the domain
of the domain  into the Riemann sphere
into the Riemann sphere 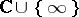 , which is a holomorphic mapping relative to the standard complex structure on
, which is a holomorphic mapping relative to the standard complex structure on 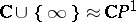 . Conversely, every holomorphic mapping
. Conversely, every holomorphic mapping 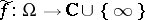 ,
,  , defines a meromorphic function
, defines a meromorphic function 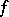 in
in  : The set of poles of
: The set of poles of 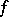 coincides with the discrete set
coincides with the discrete set 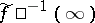 and
and 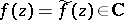 if
if 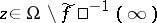 . Thus, the meromorphic functions of one variable may be identified with the holomorphic mappings (
. Thus, the meromorphic functions of one variable may be identified with the holomorphic mappings (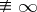 ) into the Riemann sphere.
) into the Riemann sphere.
The basic problems in the theory of meromorphic functions are those concerning the existence (and construction) of meromorphic functions with prescribed singularities.
I) One is given a (closed) discrete subset 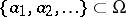 and, at each point
and, at each point 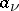 , the principal part of a Laurent expansion (cf. Laurent series)
, the principal part of a Laurent expansion (cf. Laurent series)
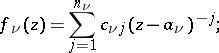 |
it is required to find a meromorphic function 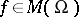 with these principal parts, i.e. a holomorphic function
with these principal parts, i.e. a holomorphic function 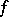 in
in 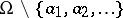 such that
such that 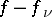 is holomorphic in a neighbourhood of
is holomorphic in a neighbourhood of 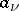 for each
for each  . If the number of points
. If the number of points 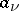 is finite, then (in a domain
is finite, then (in a domain 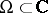 ) the problem is trivially solved by the function
) the problem is trivially solved by the function 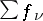 . In the general case this problem is solved by the Mittag-Leffler theorem: On every non-compact Riemann surface there exists a meromorphic function with given principal parts
. In the general case this problem is solved by the Mittag-Leffler theorem: On every non-compact Riemann surface there exists a meromorphic function with given principal parts 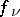 ,
, 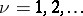 . On a compact Riemann surface (for instance, a torus) this problem has in general no solution — supplementary conditions concerning the compatibility of the principal parts must be imposed.
. On a compact Riemann surface (for instance, a torus) this problem has in general no solution — supplementary conditions concerning the compatibility of the principal parts must be imposed.
The second basic problem is conveniently formulated in the language of divisors (cf. Divisor), i.e. of mappings 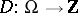 such that for every compactum
such that for every compactum 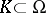 the number of points
the number of points 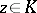 at which
at which 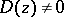 is finite (the number
is finite (the number 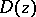 is called the multiplicity of
is called the multiplicity of 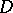 at
at  ). Divisors can explicitly be written as formal sums
). Divisors can explicitly be written as formal sums 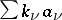 , where
, where 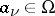 are the points at which
are the points at which  ; in the case of finitely many terms the number
; in the case of finitely many terms the number 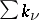 (
(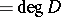 ) is called the degree of the divisor
) is called the degree of the divisor 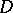 . For a meromorphic function
. For a meromorphic function 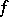 its divisor
its divisor 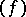 is equal to zero everywhere apart from the zeros and poles of
is equal to zero everywhere apart from the zeros and poles of 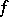 , at which the multiplicity is set equal to the order of the zero or of the pole (poles have negative orders).
, at which the multiplicity is set equal to the order of the zero or of the pole (poles have negative orders).
II) At the points of a (closed) discrete subset 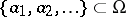 one is given "multiplicities" — integers
one is given "multiplicities" — integers 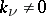 . It is required to find a meromorphic function with zeros and poles of the respective multiplicities, i.e. a holomorphic function
. It is required to find a meromorphic function with zeros and poles of the respective multiplicities, i.e. a holomorphic function 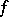 in
in 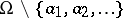 such that
such that 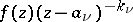 is holomorphic and does not vanish in a neighbourhood of the point
is holomorphic and does not vanish in a neighbourhood of the point  ,
, 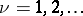 . In the case of finitely many points
. In the case of finitely many points 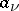 (and
(and 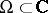 ) such a function is, for example,
) such a function is, for example, 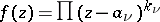 . In the general case the problem is solved by Weierstrass' theorem: On a non-compact Riemann surface
. In the general case the problem is solved by Weierstrass' theorem: On a non-compact Riemann surface  , for every given divisor
, for every given divisor 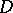 there is a meromorphic function
there is a meromorphic function 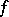 with divisor
with divisor 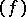 equal to
equal to 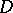 . For a compact Riemann surface
. For a compact Riemann surface  the holomorphic mapping into the Riemann sphere defined by a non-constant meromorphic function
the holomorphic mapping into the Riemann sphere defined by a non-constant meromorphic function 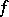 is a branched covering, and hence the function
is a branched covering, and hence the function 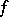 takes every value the same number of times; in particular, the number of zeros of
takes every value the same number of times; in particular, the number of zeros of 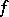 equals the number of its poles (multiplicities taken into account). Therefore, the condition
equals the number of its poles (multiplicities taken into account). Therefore, the condition 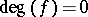 is necessary in order that problem II admits a solution on a compact Riemann surface. In general, it is not sufficient; a necessary and sufficient condition for the existence of a meromorphic function with a given divisor is given by Abel's theorem (see [2]).
is necessary in order that problem II admits a solution on a compact Riemann surface. In general, it is not sufficient; a necessary and sufficient condition for the existence of a meromorphic function with a given divisor is given by Abel's theorem (see [2]).
Let 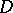 be a divisor on a compact Riemann surface
be a divisor on a compact Riemann surface  . The functions
. The functions 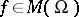 satisfying the condition
satisfying the condition 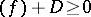 form a finite-dimensional linear space
form a finite-dimensional linear space 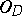 (over
(over 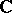 ); if
); if 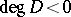 , then
, then 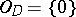 .
.
The Riemann–Roch theorem asserts that
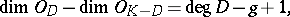 |
where 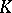 and
and 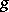 are the so-called canonical divisor and, respectively, the genus of the Riemann surface
are the so-called canonical divisor and, respectively, the genus of the Riemann surface  . From this relation one can obtain many existence theorems (if
. From this relation one can obtain many existence theorems (if 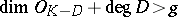 , then
, then 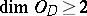 , and hence
, and hence 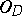 contains non-constant meromorphic functions). For example, on every compact Riemann surface
contains non-constant meromorphic functions). For example, on every compact Riemann surface  of genus
of genus  there is a meromorphic function which realizes a branched covering
there is a meromorphic function which realizes a branched covering 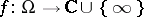 with at most
with at most 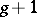 sheets.
sheets.
An important place in the theory of meromorphic functions of one complex variable is occupied by value-distribution theory (Nevanlinna theory), which studies the distribution of the roots of the equations 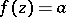 ,
, 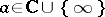 , when approaching the boundary of the domain.
, when approaching the boundary of the domain.
Meromorphic functions of several complex variables.
Let  be a domain in
be a domain in  (or an
(or an  -dimensional complex manifold) and let
-dimensional complex manifold) and let 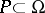 be a (complex-) analytic subset of codimension one (or empty). A holomorphic function
be a (complex-) analytic subset of codimension one (or empty). A holomorphic function 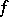 defined on
defined on 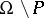 is called a meromorphic function in
is called a meromorphic function in  if for every point
if for every point 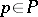 one can find an arbitrarily small neighbourhood
one can find an arbitrarily small neighbourhood 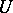 of
of 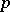 in
in  and functions
and functions 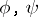 holomorphic in
holomorphic in 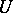 without common non-invertible factors in
without common non-invertible factors in 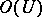 , such that
, such that 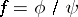 in
in  . The set
. The set 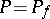 is called the polar set of the meromorphic function
is called the polar set of the meromorphic function 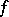 . Its subset
. Its subset 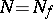 , defined locally by the condition
, defined locally by the condition 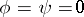 , is called the set of (points of) indeterminacy of
, is called the set of (points of) indeterminacy of 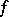 ;
; 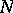 is an analytic subset of
is an analytic subset of  of (complex) codimension
of (complex) codimension 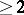 . At each point
. At each point 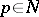 the function
the function 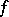 is essentially undefined: The limiting values of
is essentially undefined: The limiting values of  for
for 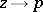 ,
, 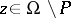 , fill up the Riemann sphere
, fill up the Riemann sphere 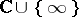 . On the other hand, at the points of
. On the other hand, at the points of 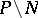 the limit
the limit 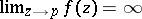 exists, and upon redefining
exists, and upon redefining 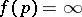 if
if  , one obtains a holomorphic mapping of
, one obtains a holomorphic mapping of 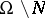 into the Riemann sphere. Conversely, if
into the Riemann sphere. Conversely, if 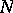 is an arbitrary (possibly empty) complex-analytic subset of
is an arbitrary (possibly empty) complex-analytic subset of  of codimension
of codimension 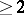 , then every holomorphic mapping
, then every holomorphic mapping 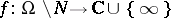 defines a meromorphic function on
defines a meromorphic function on  that is equal to
that is equal to  on
on 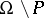 , where
, where 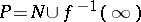 is either an analytic subset of
is either an analytic subset of  of codimension 1 or is empty. Thus, a meromorphic function
of codimension 1 or is empty. Thus, a meromorphic function 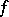 in
in  can be defined as a holomorphic mapping into the Riemann sphere defined in the complement of an analytic subset
can be defined as a holomorphic mapping into the Riemann sphere defined in the complement of an analytic subset 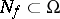 of codimension
of codimension 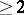 .
.
A third, completely localized, definition of meromorphic functions (equivalent to the one given above) is stated in the language of sheaves. Let 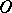 be the sheaf of germs of holomorphic functions on
be the sheaf of germs of holomorphic functions on  , and for each point
, and for each point 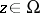 let
let 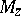 denote the field of fractions of the ring
denote the field of fractions of the ring 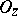 (the stalk of the sheaf
(the stalk of the sheaf 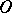 over
over  ). Then
). Then 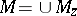 is naturally endowed with the structure of a sheaf of fields, called the sheaf of germs of meromorphic functions in
is naturally endowed with the structure of a sheaf of fields, called the sheaf of germs of meromorphic functions in  . A meromorphic function in
. A meromorphic function in  is defined as a global section of
is defined as a global section of 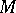 , i.e. a continuous mapping
, i.e. a continuous mapping  such that
such that 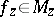 for all
for all 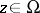 . The sets
. The sets  and
and 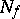 are defined as follows: If
are defined as follows: If 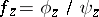 ,
, 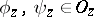 ,
, 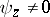 , then one may assume that
, then one may assume that 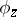 and
and 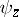 are mutually prime, i.e. they have no common non-invertible factors in
are mutually prime, i.e. they have no common non-invertible factors in 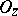 ; then
; then 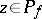 if
if 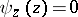 , while
, while 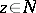 if
if 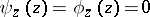 . The value at a point
. The value at a point 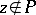 of the meromorphic function
of the meromorphic function  thus defined is
thus defined is 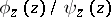 .
.
As in the one-dimensional case, the collection of all meromorphic functions in  forms a field
forms a field 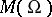 with respect to the pointwise algebraic operations with a subsequent redefinition at the removable singularities.
with respect to the pointwise algebraic operations with a subsequent redefinition at the removable singularities.
The closure 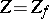 of the zero set of a meromorphic function
of the zero set of a meromorphic function 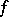 , i.e. of the set
, i.e. of the set 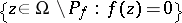 , is an analytic subset of
, is an analytic subset of  of codimension one (or empty); the set of indeterminacy is
of codimension one (or empty); the set of indeterminacy is 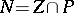 . On
. On 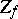 and
and 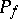 one can define the order (multiplicity) of the zeros (or poles) of the meromorphic function
one can define the order (multiplicity) of the zeros (or poles) of the meromorphic function 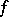 . If
. If 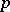 is a regular point of the analytic set
is a regular point of the analytic set 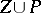 , then in some neighbourhood
, then in some neighbourhood 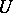 of
of 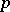 the set
the set 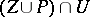 is connected and is given by an equation
is connected and is given by an equation 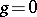 ,
, 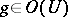 , where
, where 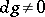 throughout
throughout 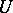 . Hence there is a maximal integer
. Hence there is a maximal integer 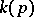 such that the function
such that the function 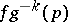 admits a holomorphic extension to
admits a holomorphic extension to 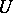 ; this number is called the order (of the zero
; this number is called the order (of the zero  if
if 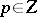 , and of the pole
, and of the pole 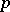 if
if 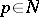 ) of the meromorphic function
) of the meromorphic function 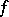 at the point
at the point 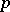 . The function
. The function 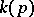 is locally constant on the set of regular points of
is locally constant on the set of regular points of 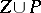 . Therefore one can attach to each meromorphic function in
. Therefore one can attach to each meromorphic function in  its divisor
its divisor 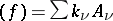 , where
, where 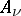 are the irreducible components of
are the irreducible components of  and
and 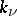 is the multiplicity (order) of
is the multiplicity (order) of 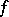 at the regular points of
at the regular points of 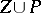 that belong to
that belong to 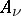 (alternative notations:
(alternative notations: 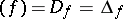 , etc.). On a compact complex manifold a meromorphic function is uniquely defined by its divisor, up to a multiplicative constant.
, etc.). On a compact complex manifold a meromorphic function is uniquely defined by its divisor, up to a multiplicative constant.
The problems solved in the one-dimensional case by the Mittag-Leffler and Weierstrass theorems are known in the higher-dimensional case as the first (additive) and the second (multiplicative) Cousin problems. Due to the complicated structure of the polar set 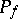 , the notion of a principal part of a meromorphic function is not defined in general, and accordingly the Cousin problems are formulated as follows.
, the notion of a principal part of a meromorphic function is not defined in general, and accordingly the Cousin problems are formulated as follows.
I) Suppose that an open covering 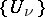 of the manifold
of the manifold  and in each
and in each 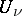 a meromorphic function
a meromorphic function  are given; it is required to find a meromorphic function
are given; it is required to find a meromorphic function 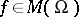 such that
such that 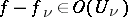 for all
for all  .
.
II) For a given divisor 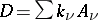 on
on  , find a meromorphic function
, find a meromorphic function 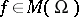 such that
such that  .
.
The conditions of solvability of these problems in the higher-dimensional case are considerably more stringent than in the one-dimensional case.
The problem of representing a meromorphic function as a quotient of two holomorphic functions is called the Poincaré problem. The strong Poincaré problem is to represent a meromorphic function as a quotient of holomorphic functions the germs of which at each point 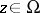 are mutually prime in
are mutually prime in 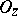 . The Poincaré problem is unsolvable on a compact connected complex manifold if there are non-constant meromorphic functions on it. However, this problem is solvable in every domain
. The Poincaré problem is unsolvable on a compact connected complex manifold if there are non-constant meromorphic functions on it. However, this problem is solvable in every domain 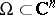 and, in fact, in an arbitrary domain on a Stein manifold (see [7]). The solvability of the strong Poincaré problem follows from that of the Cousin II problem (the converse is not true).
and, in fact, in an arbitrary domain on a Stein manifold (see [7]). The solvability of the strong Poincaré problem follows from that of the Cousin II problem (the converse is not true).
Functions 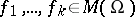 are said to be algebraically dependent if there is a polynomial
are said to be algebraically dependent if there is a polynomial 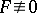 in
in 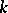 variables with complex coefficients such that
variables with complex coefficients such that 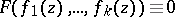 in the common domain of definition of the functions
in the common domain of definition of the functions 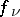 . The maximal number of algebraically-independent meromorphic functions on
. The maximal number of algebraically-independent meromorphic functions on  is called the transcendence degree of the field
is called the transcendence degree of the field  . On a compact complex manifold this number does not exceed the (complex) dimension of the manifold (Siegel's theorem); furthermore, the field
. On a compact complex manifold this number does not exceed the (complex) dimension of the manifold (Siegel's theorem); furthermore, the field 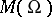 has a finite number of generators (see [6]).
has a finite number of generators (see [6]).
On concrete complex manifolds, meromorphic functions may have supplementary properties. For instance, in the complex projective space 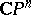 the set of indeterminacy of any non-constant meromorphic function is not empty. Every meromorphic function on a projective algebraic variety is rational, i.e. is expressible as a quotient
the set of indeterminacy of any non-constant meromorphic function is not empty. Every meromorphic function on a projective algebraic variety is rational, i.e. is expressible as a quotient 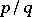 of homogeneous polynomials in homogeneous coordinates. On algebraic varieties the field
of homogeneous polynomials in homogeneous coordinates. On algebraic varieties the field 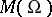 is quite rich. On the other hand, there exist complex manifolds (for example, some non-algebraic tori) on which every meromorphic function is constant. Higher-dimensional generalizations of the Riemann–Roch theorem are less effective, and existence theorems for various classes of meromorphic functions can only be obtained for some classes of complex manifolds.
is quite rich. On the other hand, there exist complex manifolds (for example, some non-algebraic tori) on which every meromorphic function is constant. Higher-dimensional generalizations of the Riemann–Roch theorem are less effective, and existence theorems for various classes of meromorphic functions can only be obtained for some classes of complex manifolds.
See also Weierstrass theorem; Mittag-Leffler theorem; Riemann–Roch theorem.
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | O. Forster, "Lectures on Riemann surfaces" , Springer (1981) (Translated from German) MR0648106 Zbl 0475.30002 |
| [3] | W.K. Hayman, "Meromorphic functions" , Clarendon Press (1964) MR0164038 Zbl 0141.07802 Zbl 0115.06203 |
| [4] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) Zbl 0799.32001 Zbl 0732.32001 Zbl 0732.30001 Zbl 0578.32001 Zbl 0574.30001 |
| [5] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) MR0344507 Zbl 0271.32001 |
| [6] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [7] | J. Kajiwara, E. Sakai, "Generalization of Levi–Oka's theorem concerning meromorphic functions" Nagoya Math. J. , 29 (1967) pp. 75–84 MR243106 |
Comments
Abel's theorem on meromorphic functions states the following. Let 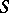 be a compact Riemann surface. A necessary and sufficient condition for a differential
be a compact Riemann surface. A necessary and sufficient condition for a differential 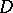 to be the divisor of a meromorphic function is that there is a singular
to be the divisor of a meromorphic function is that there is a singular 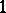 -chain
-chain 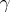 (cf. Integration on manifolds) of which
(cf. Integration on manifolds) of which 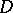 is the boundary,
is the boundary, 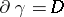 , such that
, such that  for all differentials of the first kind on
for all differentials of the first kind on 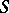 (cf. Abelian differential and Integration on manifolds). Cf. also Jacobi variety for another formulation of Abel's theorem.
(cf. Abelian differential and Integration on manifolds). Cf. also Jacobi variety for another formulation of Abel's theorem.
References
| [a1] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Sect. 10–7 MR0092855 Zbl 0078.06602 |
| [a2] | H.M. Farkas, I. Kra, "Riemann surfaces" , Springer (1980) pp. Sect. III.6 MR0583745 Zbl 0475.30001 |
Meromorphic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meromorphic_function&oldid=35167