Exponential sum estimates

Exponential sums have the form

\begin{equation*} S = \sum _ { n \in A } e ^ { 2 \pi i f ( n ) }, \end{equation*}

where $A$ is a finite set of integers and $f$ is a real-valued function (cf. also Trigonometric sum). The basic problem is to show, under suitable circumstances, that $S = o ( \# A )$ as $\# A \rightarrow \infty$. Unless there are obvious reasons to the contrary one actually expects $S$ to have order around $( \# A ) ^ { 1 / 2 }$. Exponential sums in more than one variable also occur, and much of what is stated below can be generalized to such sums.

Arithmetic sums.

There are two common types of exponential sum encountered in analytic number theory. In the first type, one starts with polynomials $g ( X ) , h ( X ) \in \mathbf{Z} [ X ]$, a positive integer modulus $q$, and a finite interval $I \subset \mathbf{R}$. One then takes $A$ as the set of integers $n \in I$ for which $\operatorname{GCD} ( h ( n ) , q ) = 1$, and sets $f ( n ) = g ( n ) \overline { h ( n ) } / q$, where $\overline { h ( n ) }$ is any integer for which $h ( n ) \overline { h ( n ) } \equiv 1 ( \operatorname { mod } q )$. When $I = ( 0 , q ]$, such a sum is called complete. When $I \subseteq ( 0 , q ]$ one may estimate the incomplete sum in terms of complete ones via the bound

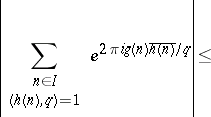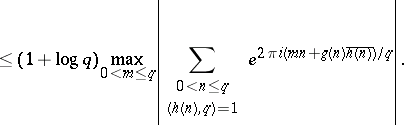Complete sums have multiplicative properties which enable one to reduce consideration to the case in which $q$ is a prime number or a power of a prime number. Moreover, Weil's Riemann hypothesis for curves over finite fields (see [a4], for example) shows that, if $q$ is prime, then

\begin{equation*} \left| \sum _ { n \in I \atop ( h ( n ) , q ) = 1 } e ^ { 2 \pi i g ( n ) \overline { h ( n )} / q } \right| \leq ( \operatorname { deg } ( g ) + \operatorname { deg } ( h ) ) \sqrt { q }, \end{equation*}

except when $g ( n ) \overline { h ( n ) }$ is constant modulo $q$. For powers of a prime number the situation is more complicated, but broadly similar. It follows that, for fixed $g$ and $h$ and $q$ prime, the incomplete sum will be $o ( \# A )$ as soon as $\# A / ( \sqrt { q }\operatorname { log } q ) \rightarrow \infty$. It is an important outstanding problem (as of 2000) to improve on this in general.

Analytic sums.

The second type of exponential sum arises when $f$ extends to a suitably smooth function on a real interval $I$. Important examples correspond to $f ( n ) = \alpha n ^ { k }$ for $k \in \mathbf{N}$, or $f ( n ) = ( t / 2 \pi ) \operatorname { log } n$, which occur in the theory of Waring's problem and the Riemann zeta-function, respectively (cf. also Waring problem; Zeta-function). Let $I = ( N , N + M ]$ with positive integers $M \leq N$. One typically imposes the condition that $f \in C ^ { \infty } [ N , N + M ]$ with

\begin{equation} \tag{a1} c _ { k } T N ^ { - k } \leq \left| f ^ { ( k ) } ( x ) \right| \leq c _ { k } ^ { \prime } T N ^ { - k } \end{equation}

\begin{equation*} ( k \in {\bf N} , N \leq x \leq N + M ), \end{equation*}

for suitable constants 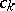, $ { c } _ { k } ^ { \prime }$. Methods due to H. Weyl (see [a5], Chap. 2), J. van der Corput (see [a1]), I.M. Vinogradov and N.M. Korobov (see [a3], Chap. 6), and E. Bombieri and H. Iwaniec (see [a2]) have been used for sums of this type.

Van der Corput's method.

Of the above approaches, the method of van der Corput is perhaps the most versatile. It is based on two processes, which convert the original sum $S$ into other sums. The A-process uses the inequality

\begin{equation*} \left| \sum _ { M < n \leq M + N } e ^ { 2 \pi i f ( n ) } \right| ^ { 2 } \ll \end{equation*}

\begin{equation*} \ll \frac { N ^ { 2 } } { H } + \frac { N } { H } \sum _ { 1 \leq h \leq H } \left| \sum_ { M < n \leq M + N - h } e ^ { 2 \pi i ( \, f ( n + h ) - f ( n ) ) } \right|, \end{equation*}

where $H \in \mathbf{N}$ satisfies $H \leq N$. This has the effect of replacing $f$ by a function $f ( x + h ) - f ( x )$ which satisfies (a1) with a smaller value of $T$. To describe the B-process it is assumed that $f ^ { \prime }$ is decreasing, and one writes $f ^ { \prime } ( M + N ) = A$, $f ^ { \prime } ( N ) = B$ and $f ^ { \prime } ( x _ { m } ) = m$ for $A < m \leq A + B$. The B-process then derives from the estimate

\begin{equation*} \sum _ { M < n \leq M + N } e ^ { 2 \pi i f ( n ) } = \end{equation*}

\begin{equation*} = e ^ { - i \pi / 4 } \sum _ { A < m \leq A + B } | f ^ { \prime } ( x _ { m } ) | ^ { - 1 / 2 } e ^ { 2 \pi i ( f ( x _ { m } ) - m x _ { m } ) } + \end{equation*}

\begin{equation*} + O ( T ^ { 1 / 3 } ) + O ( N ^ { 2 } T ^ { - 1 / 2 } ), \end{equation*}

which may be viewed as a form of the Poisson summation formula. When $T \ll N ^ { 2 }$, the B-process transforms $S$ into a sum with the same value of $T$ but a shorter range. In applications one uses the A-process repeatedly, with various values of $H$, until one has a sum to which the B-process can be applied effectively. One may then estimate the resulting shorter sum either via a trivial bound or by repeating the argument. In particular, $k - 2$ iterations of the A-process, followed by the B-process and a trivial estimate lead to van der Corput's $k$th derivative estimate: Let $k \geq 2$ be an integer, and let $f \in C ^ { k } [ N , N + M ]$ with $M$, $N$ integers. Suppose that $0 < \lambda _ { k } \leq | f ^ { ( k ) } ( x ) | \leq A \lambda _ { k }$ on $[ N , N + M ]$. Then, if $K = 2 ^ { k - 1 }$, one has

\begin{equation*} \sum _ { M < n \leq M + N } e ^ { 2 \pi i f ( n ) } \ll \end{equation*}

\begin{equation*} \ll A ^ { 2 / K } N \lambda _ { k } ^ { 1 / ( 2 K - 2 ) } + M ^ { 1 - 2 / K } \lambda _ { k } ^ { - 1 / ( 2 K - 2 ) }, \end{equation*}

uniformly in $k$.

Exponent pairs.

Many bounds of the form $S \ll ( T / N ) ^ { p } N ^ { q }$ subject to (a1), or similar slightly stronger conditions, have been proved. If one has such a bound, one says that $( p , q )$ is an exponent pair. Thus, the van der Corput third-derivative estimate shows that $( 1 / 6,2 / 3 )$ is an exponent pair. The case $q = p + 1 / 2$ is of particular interest, since it leads to a bound for the Riemann zeta-function, of the form $\zeta ( 1 / 2 + i t ) \ll t ^ { p } \operatorname { log } t$ for $t \geq 2$. Although van der Corput's method leads to a rich source of exponent pairs, better results can be derived by more complicated methods. Thus, M.N. Huxley [a2], Chap. 17, shows that $( p , p + 1 / 2 )$ is an exponent pair whenever $p > 89 / 570$, using the Bombieri–Iwaniec method. It is conjectured that $( p , p + 1 / 2 )$ is an exponent pair for any positive $p$. This can be seen as a generalization of the Lindelöf hypothesis for the Riemann zeta-function.

The Vinogradov–Korobov method.

When (a1) holds with $T$ larger than about $N ^ { 20 }$, the van der Corput method is inferior to that given by Vinogradov and Korobov. This range of values is important in establishing zero-free regions for the Riemann zeta-function, for example. The method reduces the problem to an estimate for the number of solutions of the simultaneous equations $\sum _ { i = 1 } ^ { k } m _ { i } ^ { h } = \sum _ { i = 1 } ^ { k } n _ { i } ^ { h }$ for $1 \leq h \leq H$ with positive integer variables $m _ { i } , n _ { i } \leq P$. This is provided by Vinogradov's mean value theorem (cf. also Vinogradov method).

References

[a1]	S.W. Graham, G. Kolesnik, "Van der Corput's method for exponential sums" , London Math. Soc. Lecture Notes , 126 , Cambridge Univ. Press (1991)
[a2]	M.N. Huxley, "Area, lattice points and exponential sums" , London Math. Soc. Monographs , 13 , Clarendon Press (1996)
[a3]	A. Ivić, "The Riemann zeta-function" , Wiley (1985)
[a4]	W.M. Schmidt, "Equations over finite fields. An elementary approach" , Lecture Notes in Mathematics , 536 , Springer (1976)
[a5]	R.C. Vaughan, "The Hardy–Littlewood method" , Tracts in Math. , 80 , Cambridge Univ. Press (1981)
[a6]	N.M. Korobov, "Exponential sums and their applications" , Kluwer Acad. Publ. (1992)