Barycentric coordinates
Coordinates of a point in an  -dimensional vector space
-dimensional vector space  , with respect to some fixed system
, with respect to some fixed system  of points that do not lie in an
of points that do not lie in an  -dimensional subspace. Every point
-dimensional subspace. Every point  can uniquely be written as
can uniquely be written as
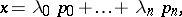 |
where  are real numbers satisfying the condition
are real numbers satisfying the condition  . The point
. The point  is by definition the centre of gravity of the masses
is by definition the centre of gravity of the masses  located at the points
located at the points  . The numbers
. The numbers 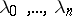 are called the barycentric coordinates of the point
are called the barycentric coordinates of the point  ; the point with barycentric coordinates
; the point with barycentric coordinates  is called the barycentre. Barycentric coordinates were introduced by A.F. Möbius in 1827, [1], as an answer to the question about the masses to be placed at the vertices of a triangle so that a given point is the centre of gravity of these masses. Barycentric coordinates are a special case of homogeneous coordinates; they are affine invariants.
is called the barycentre. Barycentric coordinates were introduced by A.F. Möbius in 1827, [1], as an answer to the question about the masses to be placed at the vertices of a triangle so that a given point is the centre of gravity of these masses. Barycentric coordinates are a special case of homogeneous coordinates; they are affine invariants.
Barycentric coordinates of a simplex are used in algebraic topology [2]. Barycentric coordinates of a point of an  -dimensional simplex
-dimensional simplex  with respect to its vertices
with respect to its vertices 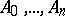 is the name given to its (ordinary) Cartesian coordinates in the basis of the vectors
is the name given to its (ordinary) Cartesian coordinates in the basis of the vectors 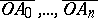 , where
, where 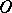 is any point that does not lie in the
is any point that does not lie in the  -dimensional subspace carrying
-dimensional subspace carrying 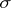 (if it is considered that
(if it is considered that 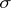 lies in some Euclidean space, then the definition does not depend on the point
lies in some Euclidean space, then the definition does not depend on the point  ), or to projective coordinates with respect to
), or to projective coordinates with respect to  in the projective completion of the subspace containing
in the projective completion of the subspace containing 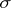 . The barycentric coordinates of the points of a simplex are non-negative and their sum is equal to one. If the
. The barycentric coordinates of the points of a simplex are non-negative and their sum is equal to one. If the 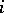 -th barycentric coordinate becomes zero, this means that the point lies at the side of the simplex
-th barycentric coordinate becomes zero, this means that the point lies at the side of the simplex  opposite to the vertex
opposite to the vertex  . This makes it possible to consider the barycentric coordinates of the points of a geometric complex with respect to all of its vertices. Barycentric coordinates are used to construct the barycentric subdivision of a complex.
. This makes it possible to consider the barycentric coordinates of the points of a geometric complex with respect to all of its vertices. Barycentric coordinates are used to construct the barycentric subdivision of a complex.
Barycentric coordinates of abstract complexes are formally defined in an analogous manner [3].
References
| [1] | A.F. Möbius, "Der barycentrische Kalkul" , Gesammelte Werke , 1 , Hirzel , Leipzig (1885) |
| [2] | L.S. Pontryagin, "Grundzüge der kombinatorischen Topologie" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
Barycentric coordinates. E.G. Sklyarenko (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Barycentric_coordinates&oldid=15139