Two-dimensional knot
A class of isotopic imbeddings of the two-dimensional sphere  in the four-dimensional one
in the four-dimensional one  . The condition of local planarity is usually imposed. The method of study consists in considering sections of
. The condition of local planarity is usually imposed. The method of study consists in considering sections of  by a bundle of three-dimensional parallel planes. The fundamental problem is whether or not the knot will be trivial if its group
by a bundle of three-dimensional parallel planes. The fundamental problem is whether or not the knot will be trivial if its group 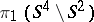 is isomorphic to
is isomorphic to 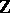 . It is known that in such a case the complement
. It is known that in such a case the complement 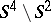 has the homotopy type of
has the homotopy type of 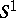 .
.
A  -ribbon in
-ribbon in  is the image
is the image 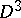 of an immersion
of an immersion 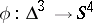 , where
, where  is the three-dimensional disc, such that: 1)
is the three-dimensional disc, such that: 1) 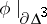 is an imbedding; 2) the self-intersection of
is an imbedding; 2) the self-intersection of  consists of a finite number of pairwise non-intersecting two-dimensional discs
consists of a finite number of pairwise non-intersecting two-dimensional discs  ; and 3) the pre-image
; and 3) the pre-image 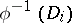 of each disc
of each disc  is a union of two discs
is a union of two discs  and
and 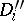 such that
such that
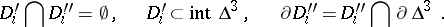 |
The image of the boundary  is a two-dimensional knot in
is a two-dimensional knot in  . The knots thus obtained are said to be ribbon knots. This is one of the most thoroughly studied class of two-dimensional knots. Any two-dimensional ribbon knot is the boundary of some three-dimensional submanifold of the sphere
. The knots thus obtained are said to be ribbon knots. This is one of the most thoroughly studied class of two-dimensional knots. Any two-dimensional ribbon knot is the boundary of some three-dimensional submanifold of the sphere  which is homeomorphic either to the disc
which is homeomorphic either to the disc  or to the connected sum of some number of
or to the connected sum of some number of 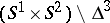 . A two-dimensional ribbon knot is trivial if and only if the fundamental group of its complement is isomorphic to
. A two-dimensional ribbon knot is trivial if and only if the fundamental group of its complement is isomorphic to 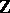 . A group
. A group 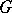 is the group of some two-dimensional ribbon knot in
is the group of some two-dimensional ribbon knot in  if and only if it has a Wirtinger presentation (i.e. a presentation
if and only if it has a Wirtinger presentation (i.e. a presentation  , where each relation has the form
, where each relation has the form  ) in which the number of relations is one smaller than the number of generators and
) in which the number of relations is one smaller than the number of generators and 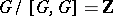 .
.
The class of groups of all two-dimensional knots has not yet been fully described. It is known that this class is wider than that of the one-dimensional knots in  but smaller than the class of groups of
but smaller than the class of groups of 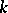 -dimensional knots in
-dimensional knots in 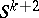 ,
,  . The latter class has been fully characterized (cf. Multi-dimensional knot). The following properties are displayed by two-dimensional knot groups (but not, in general, by the groups of three-dimensional knots in
. The latter class has been fully characterized (cf. Multi-dimensional knot). The following properties are displayed by two-dimensional knot groups (but not, in general, by the groups of three-dimensional knots in  ):
):
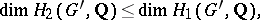 |
where 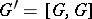 is the commutator subgroup; on the finite group
is the commutator subgroup; on the finite group 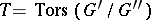 there exists a non-degenerate symmetric form
there exists a non-degenerate symmetric form 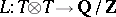 such that for any
such that for any  ,
,  one has
one has 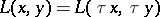 , where
, where  is the automorphism induced in
is the automorphism induced in  by conjugation with the element
by conjugation with the element 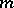 .
.
The calculation of 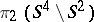 has been done only for special types of two-dimensional knots, e.g. those obtained by Artin's construction, ribbon knots and fibred knots.
has been done only for special types of two-dimensional knots, e.g. those obtained by Artin's construction, ribbon knots and fibred knots.
Two-dimensional knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-dimensional_knot&oldid=19122