Thom-Boardman singularities
Consider a smooth mapping  , where
, where  and
and  are smooth manifolds of dimension
are smooth manifolds of dimension  and
and  , respectively (by smooth one understands: class
, respectively (by smooth one understands: class  ; cf. also Manifold). In order to understand the local structure of
; cf. also Manifold). In order to understand the local structure of  , it is natural to distinguish among points
, it is natural to distinguish among points  according to the rank of the derivative
according to the rank of the derivative  , where
, where 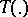 denotes the tangent space. For
denotes the tangent space. For 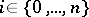 , set:
, set:
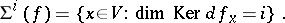 |
Using local coordinates on 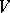 and
and  , this set is defined locally by the vanishing of the
, this set is defined locally by the vanishing of the 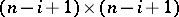 -minors of the
-minors of the 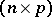 -matrix of first-order partial derivatives of
-matrix of first-order partial derivatives of 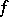 . If one assumes that
. If one assumes that 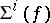 is a smooth submanifold of
is a smooth submanifold of 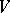 , for
, for 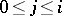 one can define
one can define
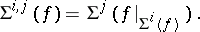 |
This can be visualized as follows: at a point  there are two vector subspaces of
there are two vector subspaces of 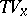 , namely
, namely 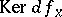 and
and 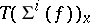 . Then
. Then 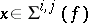 if and only if the intersection of these two subspaces has dimension
if and only if the intersection of these two subspaces has dimension 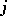 .
.
Again, if one assumes that 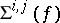 is a smooth submanifold, then one can define a subset
is a smooth submanifold, then one can define a subset 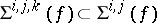 , etc. At the end, one has partitioned the manifold
, etc. At the end, one has partitioned the manifold  into a collection of locally closed submanifolds, such that the restriction of
into a collection of locally closed submanifolds, such that the restriction of 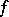 to each submanifold is of maximal rank; in fact, if the local equations defining the various submanifolds of the collection are of maximal rank, it turns out that for
to each submanifold is of maximal rank; in fact, if the local equations defining the various submanifolds of the collection are of maximal rank, it turns out that for 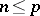 the restriction of
the restriction of 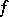 to each submanifold is an immersion, while for
to each submanifold is an immersion, while for  the same holds except at the points of rank
the same holds except at the points of rank 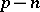 , where it is a submersion.
, where it is a submersion.
This program has been initiated by R. Thom in his seminal paper [a9], inspired by earlier work of H. Whitney [a10]. Thom handles completely the first-order case, by showing that for a generic mapping (i.e. for mappings in a dense subset of all smooth mappings from 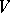 to
to  ),
), 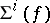 is a locally closed submanifold of codimension
is a locally closed submanifold of codimension 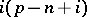 of
of 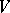 , and that for the closure one has:
, and that for the closure one has:
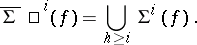 |
This is done by writing the mapping locally as 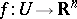 ,
, 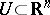 open, then associating to each
open, then associating to each 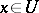 the graph
the graph 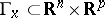 of the derivative
of the derivative 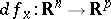 . Clearly,
. Clearly, 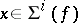 if and only if
if and only if 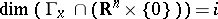 , a condition defining a Schubert variety
, a condition defining a Schubert variety 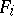 in the Grassmann manifold
in the Grassmann manifold 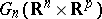 of
of  -planes in
-planes in  . Thus,
. Thus, 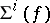 is seen locally as the pull-back of
is seen locally as the pull-back of 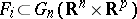 by the mapping
by the mapping 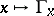 .
.
This approach is exemplary, because it presents the singular locus 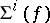 as the pull-back of a universal situation, namely
as the pull-back of a universal situation, namely 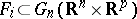 ; it is then straightforward to show that for most mappings
; it is then straightforward to show that for most mappings 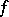 , the induced local mappings
, the induced local mappings 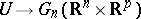 are transversal to
are transversal to 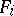 , and hence that
, and hence that  is a locally closed smooth submanifold of codimension
is a locally closed smooth submanifold of codimension  of
of  . Moreover, this approach can serve as basis for the computation of the cohomology class that is Poincaré dual to
. Moreover, this approach can serve as basis for the computation of the cohomology class that is Poincaré dual to 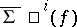 , which can be interpreted as the first obstruction to having a homotopy from
, which can be interpreted as the first obstruction to having a homotopy from 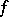 to a mapping
to a mapping 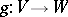 for which
for which  (see [a9], p. 80, or [a5], Prop. 1.3; the dual classes for second-order singularities have been computed in [a7] and [a6]).
(see [a9], p. 80, or [a5], Prop. 1.3; the dual classes for second-order singularities have been computed in [a7] and [a6]).
The complete proof that the process of decomposition of the source of a generic smooth mapping can be carried out successfully has been given by J.M. Boardman [a1]. See Singularities of differentiable mappings for the notions of jet space 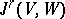 and
and  -jet extension
-jet extension  of a mapping
of a mapping 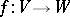 , used below.
, used below.
For smooth manifolds  and
and 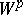 , and integers
, and integers 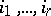 , with
, with 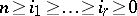 , one defines the subsets
, one defines the subsets 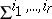 of the space of
of the space of  -jets
-jets  ; it can be proved that these are locally closed smooth submanifolds, and that if
; it can be proved that these are locally closed smooth submanifolds, and that if 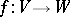 is a mapping whose jet extensions
is a mapping whose jet extensions 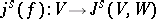 are transversal to
are transversal to 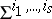 ,
, 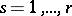 , then, setting
, then, setting
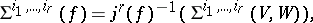 |
one obtains:
 |
 |
The codimension of  equals
equals
 |
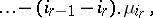 |
where 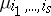 is the number of sequences
is the number of sequences 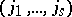 satisfying
satisfying
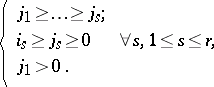 |
Moreover, local equations for 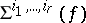 can be given explicitly, in terms of the ideal generated by the components of
can be given explicitly, in terms of the ideal generated by the components of 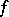 , in some local coordinates, and its Jacobian extensions, an operation which adds to an ideal of functions certain minors of the matrix of their first-order derivatives.
, in some local coordinates, and its Jacobian extensions, an operation which adds to an ideal of functions certain minors of the matrix of their first-order derivatives.
The 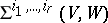 are called Thom–Boardman singularities.
are called Thom–Boardman singularities.
An alternative, more concise approach to Thom–Boardman singularities has been given later by J.N. Mather [a2], and an algebraic approach can be found in [a4].
Thom's transversality theorem [a8] implies that the set of mappings that are transversal to all possible Thom–Boardman singularities, that one may call generic mappings, is dense in the space of all mappings from 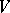 to
to 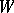 . So now one may ask how useful are Thom–Boardman singularities in the understanding of generic mappings.
. So now one may ask how useful are Thom–Boardman singularities in the understanding of generic mappings.
In some cases, they allow a full classification. This is so, for example, if  and
and 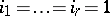 , or
, or  and
and  ,
,  , by a result of B. Morin [a3]; for
, by a result of B. Morin [a3]; for 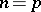 and
and 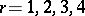 one finds the catastrophes of the fold, the cusp, the swallowtail, and the butterfly, respectively (see Thom catastrophes).
one finds the catastrophes of the fold, the cusp, the swallowtail, and the butterfly, respectively (see Thom catastrophes).
In general, Thom–Boardman singularities allow a very useful first approach to the understanding of the structure of a mapping; however, they are not fine enough to provide an, even coarse, classification. Indeed, as pointed out by I.R. Porteous [a6], a generic mapping 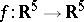 can present the singularities
can present the singularities 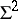 and
and  , both of dimension
, both of dimension 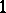 , and some isolated points of
, and some isolated points of 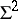 , called parabolic
, called parabolic  -points by Porteous, can be in the closure of
-points by Porteous, can be in the closure of 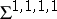 ; the structure of such a mapping is definitely different at
; the structure of such a mapping is definitely different at 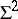 -parabolic and
-parabolic and  -non-parabolic points. Similar phenomena occur in other dimensions.
-non-parabolic points. Similar phenomena occur in other dimensions.
In fact, Thom–Boardman singularities provide a partition of the source of a generic mapping into locally closed submanifolds, but the closure of a submanifold is not necessarily a union of similar submanifolds.
When studying the equations of Thom–Boardman singularities, an interesting device shows up: the intrinsic derivative, first studied by Porteous (see [a5]). In general, derivatives of order higher than 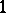 are not intrinsic, in the sense that are affected by higher derivatives of coordinate changes, not only the linear part of them. However, it turns out that if
are not intrinsic, in the sense that are affected by higher derivatives of coordinate changes, not only the linear part of them. However, it turns out that if  , then a suitable combination of the first
, then a suitable combination of the first 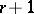 derivatives, restricted to appropriate subspaces, is intrinsic. The simplest case is that of the second intrinsic derivative; if
derivatives, restricted to appropriate subspaces, is intrinsic. The simplest case is that of the second intrinsic derivative; if 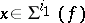 , then the bilinear mapping induced by the second derivative,
, then the bilinear mapping induced by the second derivative,
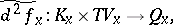 |
where 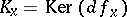 ,
, 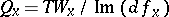 is intrinsic, as one can check easily. In the special case of a function
is intrinsic, as one can check easily. In the special case of a function 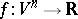 , if
, if 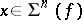 is a critical point, then
is a critical point, then 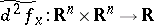 is the well-known Hessian bilinear form of
is the well-known Hessian bilinear form of 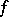 at
at  (cf. also Hessian matrix), whose signature determines completely the local structure of
(cf. also Hessian matrix), whose signature determines completely the local structure of 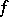 near
near  .
.
The intrinsic derivative can be used to refine Thom–Boardman singularities; for example, for a generic mapping  :
:
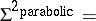 |
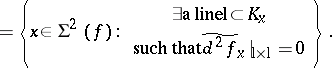 |
An inductive definition of the intrinsic derivatives is provided in [a1]; so far, it has not been tried to refine systematically Thom–Boardman singularities using them.
References
| [a1] | J.M. Boardman, "Singularities of differentiable maps" Publ. Math. IHES , 33 (1967) pp. 383–419 |
| [a2] | J.N. Mather, "On Thom–Boardman singularities" M.M. Peixoto (ed.) , Dynamical Systems, Proc. Symp. Univ. Bahia, 1971 , Acad. Press (1973) pp. 233–248 |
| [a3] | B. Morin, "Formes canoniques des singularités d'une application différentiable" C.R. Acad. Sci. Paris , 260 (1965) pp. 5662–5665; 6503–6506 |
| [a4] | B. Morin, "Calcul jacobien" Thèse Univ. Paris–Sud centre d'Orsay (1972) |
| [a5] | I.R. Porteous, "Simple singularities of maps" , Proc. Liverpool Singularities Symp. , Lecture Notes Math. , 192 , Springer (1971) pp. 286–312 |
| [a6] | I.R. Porteous, "The second order decomposition of 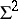 " Topology , 11 (1972) pp. 325–334 " Topology , 11 (1972) pp. 325–334 |
| [a7] | F. Ronga, "Le calcul des classes duales aux singularités de Boardman d'ordre deux" Comment. Math. Helvetici , 47 (1972) pp. 15–35 |
| [a8] | R. Thom, "Un lemme sur les applications différentiables" Bol. Soc. Mat. Mexicana (1956) pp. 59–71 |
| [a9] | R. Thom, "Les singularités des applications différentiables" Ann. Inst. Fourier (Grenoble) , 6 (1955/6) pp. 43–87 |
| [a10] | H. Whitney, "On singularities of mappings of euclidean spaces: I. Mappings of the plane into the plane" Ann. of Math. , 62 (1955) pp. 374–410 |
Thom-Boardman singularities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom-Boardman_singularities&oldid=17236