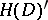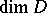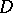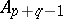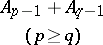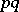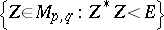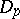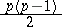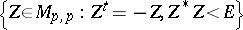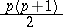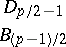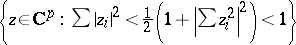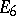Symmetric domain
A complex manifold  isomorphic to a bounded domain in
isomorphic to a bounded domain in 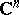 and such that, for every point
and such that, for every point 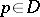 , there is an involutory holomorphic transformation
, there is an involutory holomorphic transformation 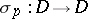 with
with 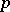 as unique fixed point. A symmetric domain is a Hermitian symmetric space of negative curvature with respect to the Bergman metric (cf. Bergman kernel function). Its automorphism group is contained, as a complex manifold, in the group of motions and has the same connected component
as unique fixed point. A symmetric domain is a Hermitian symmetric space of negative curvature with respect to the Bergman metric (cf. Bergman kernel function). Its automorphism group is contained, as a complex manifold, in the group of motions and has the same connected component 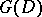 , which is a non-compact real semi-simple Lie group without centre. The stationary subgroup
, which is a non-compact real semi-simple Lie group without centre. The stationary subgroup 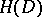 of
of 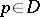 in
in 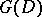 is a connected compact Lie group with one-dimensional centre. As a real manifold, a symmetric domain is diffeomorphic to
is a connected compact Lie group with one-dimensional centre. As a real manifold, a symmetric domain is diffeomorphic to 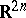 .
.
Every symmetric domain is uniquely decomposable as a direct product of irreducible symmetric domains, and these are listed in the following table (where 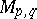 denotes the space of complex
denotes the space of complex 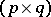 -matrices).'
-matrices).'
<tbody> </tbody>
|
A symmetric domain of type III can be represented as the Siegel upper half-plane:
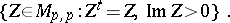 |
Its points parametrize principally polarized Abelian varieties. The other symmetric domains can also be represented as Siegel domains (cf. Siegel domain) of the first or second kind (see [2]).
References
| [1] | C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955) |
| [2] | I.I. [I.I. Pyatetskii-Shapiro] Piatetski-Shapiro, "Automorphic functions and the geometry of classical domains" , Gordon & Breach (1969) (Translated from Russian) |
| [3] | E. Cartan, "Domains bornés homogènes de l'espace de  variables complexes" Abh. Math. Sem. Univ. Hamburg , 1 (1935) pp. 116–162 variables complexes" Abh. Math. Sem. Univ. Hamburg , 1 (1935) pp. 116–162 |
| [4] | D. Drucker, "Exceptional Lie algebras and the structure of hermitian symmetric spaces" , Amer. Math. Soc. (1978) |
Comments
The stationary subgroup 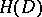 has one-dimensional centre if and only if the symmetric domain is irreducible.
has one-dimensional centre if and only if the symmetric domain is irreducible.
References
| [a1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. Chapt. X |
Symmetric domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_domain&oldid=16315