Subprojective space
One of the generalizations of spaces of constant curvature (of projective space). One defines a 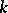 -fold projective space with an affine connection and expresses its geodesic lines in some coordinate system by a system of
-fold projective space with an affine connection and expresses its geodesic lines in some coordinate system by a system of 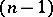 equations of which exactly
equations of which exactly 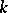 are linear. When
are linear. When 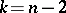 , the geodesic lines are planar, and are situated in two-dimensional Euclidean planes, and the space is said to be subprojective if all these two-dimensional Euclidean planes pass through a common point or are parallel in one direction (the common point is infinitely distant).
, the geodesic lines are planar, and are situated in two-dimensional Euclidean planes, and the space is said to be subprojective if all these two-dimensional Euclidean planes pass through a common point or are parallel in one direction (the common point is infinitely distant).
Let 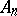 be an
be an  -dimensional subprojective space with a torsion-free affine connection. With respect to a projective coordinate system
-dimensional subprojective space with a torsion-free affine connection. With respect to a projective coordinate system  of
of 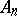 , the coefficients of the connection take the form
, the coefficients of the connection take the form
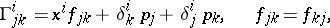 |
where  are the Kronecker symbols and
are the Kronecker symbols and
 |
In this coordinate system, all two-dimensional Euclidean planes on which the geodesic lines of 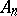 are situated pass through the coordinate origin.
are situated pass through the coordinate origin.
In general, in a subprojective space 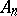 there exists a canonical coordinate system
there exists a canonical coordinate system  in which the coefficients of the connection take the simplest form
in which the coefficients of the connection take the simplest form
 |
A Riemannian subprojective space 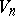 is defined in the same way; its metric reduces to one of three possible forms:
is defined in the same way; its metric reduces to one of three possible forms:
 |
where
1) 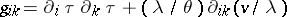 ,
,
2) 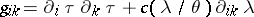 ,
, 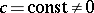 ; here
; here 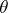 is an arbitrary function in the coordinates
is an arbitrary function in the coordinates  ,
, 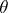 is a function of the variable
is a function of the variable 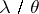 ,
,  is a quadratic form in the
is a quadratic form in the  ,
, 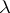 in 1) is a linear form and in 2) it is the square root of a quadratic form that is not a complete square.
in 1) is a linear form and in 2) it is the square root of a quadratic form that is not a complete square.
3) The exceptional case
 |
where  ,
, 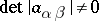 ,
, 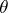 is a homogeneous function of degree one in
is a homogeneous function of degree one in 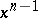 and
and 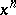 , and
, and 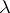 and
and  are functions related by
are functions related by
 |
The functions 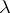 and
and  are not homogeneous of the first degree.
are not homogeneous of the first degree.
All three cases can be reduced to a uniform expression by the choice of coordinates  :
:
1) 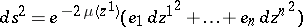 ,
,
2)  ,
,  ,
,
3)  ,
, 
 . All Riemannian subprojective spaces
. All Riemannian subprojective spaces 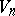 are conformal Euclidean spaces (cf. Conformal Euclidean space). Riemannian subprojective spaces belong to the class of semi-reducible Riemannian spaces and their metrics have a special structure.
are conformal Euclidean spaces (cf. Conformal Euclidean space). Riemannian subprojective spaces belong to the class of semi-reducible Riemannian spaces and their metrics have a special structure.
Tensor criteria for conformal Euclidean subprojective spaces exist, distinguishing them from the class of all conformal Euclidean spaces. Every subprojective space 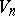 (apart from the case 3)) can be realized as a hypersurface in a Euclidean space
(apart from the case 3)) can be realized as a hypersurface in a Euclidean space  in the case 1), or as a hypersurface of rotation in
in the case 1), or as a hypersurface of rotation in  in the case 2). The converse is also true: Every hypersurface of rotation around a non-isotropic axis in a Euclidean space
in the case 2). The converse is also true: Every hypersurface of rotation around a non-isotropic axis in a Euclidean space  ,
,  , is a Riemannian subprojective space with a metric of the form 2).
, is a Riemannian subprojective space with a metric of the form 2).
Motions in Riemannian subprojective spaces are defined in the usual way. The subprojective spaces 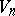 are characterized by the fact that if
are characterized by the fact that if 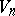 is not a space of constant curvature, then it permits a maximal intransitive group of motions of order
is not a space of constant curvature, then it permits a maximal intransitive group of motions of order  , and, conversely, every Riemannian space
, and, conversely, every Riemannian space 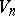 that permits a maximal intransitive group of order
that permits a maximal intransitive group of order  is a subprojective space. Riemannian subprojective spaces
is a subprojective space. Riemannian subprojective spaces 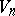 are maximally-mobile non-Einsteinian spaces (spaces of constant curvature occupy the same position among the Einstein spaces).
are maximally-mobile non-Einsteinian spaces (spaces of constant curvature occupy the same position among the Einstein spaces).
The concept of a subprojective space permits the following generalizations: A space 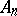 with an affine connection is called a generalized subprojective space if its geodesic lines lie in Euclidean planes
with an affine connection is called a generalized subprojective space if its geodesic lines lie in Euclidean planes  ,
,  , that pass through a fixed plane
, that pass through a fixed plane  (at a finite or infinite distance).
(at a finite or infinite distance).
References
| [1] | V.F. Kagan, "Subprojective spaces" , Moscow (1961) (In Russian) |
Comments
References
| [a1] | J.A. Schouten, "Ricci-calculus. An introduction to tensor analysis and its geometrical applications" , Springer (1954) (Translated from German) |
Subprojective space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subprojective_space&oldid=15475