Solèr theorem
Let 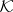 be a
be a  -field,
-field,  a left vector space over
a left vector space over 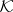 , and
, and 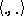 an orthomodular form on
an orthomodular form on 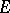 that has an infinite orthonormal sequence (see below for definitions). Then Solèr's theorem states that
that has an infinite orthonormal sequence (see below for definitions). Then Solèr's theorem states that 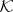 must be
must be 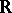 ,
, 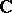 , or
, or  , and
, and 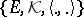 is the corresponding Hilbert space [a7].
is the corresponding Hilbert space [a7].
Definitions.
A  -field
-field  is a (commutative or non-commutative) field with involution. (An involution is a mapping
is a (commutative or non-commutative) field with involution. (An involution is a mapping 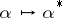 of
of 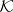 onto itself that satisfies
onto itself that satisfies 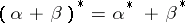 ,
, 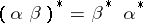 , and
, and 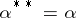 for all
for all 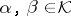 .)
.)
The set of real numbers 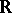 with the identity involution, the set of complex numbers
with the identity involution, the set of complex numbers 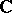 with complex conjugation as involution, and the set of real quaternions
with complex conjugation as involution, and the set of real quaternions  with the usual quaternionic conjugation as involution are the three classical examples of
with the usual quaternionic conjugation as involution are the three classical examples of  -fields.
-fields.
A Hermitian form 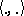 on a left vector space
on a left vector space 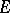 over a
over a  -field
-field 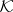 is a mapping
is a mapping  that associates to every pair of vectors
that associates to every pair of vectors 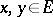 a scalar
a scalar 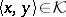 in accordance with the following rules:
in accordance with the following rules:
i) it is linear in the first variable and conjugate linear with respect to  in the second variable (in short: it is conjugate bilinear);
in the second variable (in short: it is conjugate bilinear);
ii) 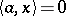 or
or 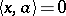 for all
for all  implies
implies 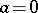 (in short: it is regular);
(in short: it is regular);
iii) 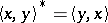 for all
for all 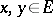 (the Hermitian property). Two vectors
(the Hermitian property). Two vectors  ,
, 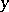 in a Hermitian space
in a Hermitian space 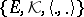 are orthogonal when
are orthogonal when 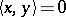 . A sequence
. A sequence 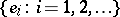 of non-zero vectors is called orthogonal when
of non-zero vectors is called orthogonal when 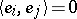 for
for 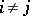 ; and it is called orthonormal when also
; and it is called orthonormal when also 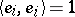 ,
, 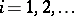 .
.
Given a non-empty subset 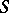 of
of 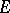 , the symbol
, the symbol 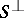 stands for the set of those elements in
stands for the set of those elements in 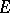 that are orthogonal to every element of
that are orthogonal to every element of 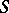 :
:
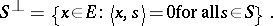 |
A subspace 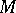 of
of 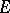 is called closed when
is called closed when 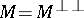 . A Hermitian space is orthomodular when
. A Hermitian space is orthomodular when 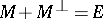 for every closed subspace
for every closed subspace 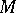 ; in symbols:
; in symbols:  and
and 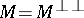 imply
imply 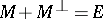 .
.
A Hilbert space is a Hermitian space over 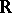 ,
, 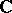 , or
, or  whose form is positive definite, i.e.,
whose form is positive definite, i.e.,  implies
implies 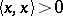 , and which is complete with respect to the metric
, and which is complete with respect to the metric 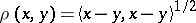 derived from that form. The well-known projection theorem asserts that a Hilbert space is orthomodular.
derived from that form. The well-known projection theorem asserts that a Hilbert space is orthomodular.
History.
There are two conclusions in Solèr's theorem:
1) the underlying  -field is
-field is 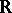 ,
, 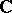 or
or  ; and
; and
2) the resulting space is metrically complete. The first conclusion, which materializes 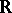 ,
, 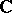 , and
, and  out of all possible
out of all possible  -fields, is Solèr's contribution. Of the two conclusions, the first is by far the most difficult to establish, the most striking in its appearance, and the most far-reaching in its consequences. The metric completeness was actually surmised earlier by C. Piron [a5], then proved by I. Amemiya and H. Araki [a1]. Keller's example of a "non-classical" Hilbert space shows that Solèr's result no longer holds if only orthomodularity is assumed [a3]. Prior to Solèr's definitive result, a vital contribution was made by W.J. Wilbur [a8].
-fields, is Solèr's contribution. Of the two conclusions, the first is by far the most difficult to establish, the most striking in its appearance, and the most far-reaching in its consequences. The metric completeness was actually surmised earlier by C. Piron [a5], then proved by I. Amemiya and H. Araki [a1]. Keller's example of a "non-classical" Hilbert space shows that Solèr's result no longer holds if only orthomodularity is assumed [a3]. Prior to Solèr's definitive result, a vital contribution was made by W.J. Wilbur [a8].
M.P. Solèr is a student of the late Professor H. Gross. This result is her 1994 doctoral thesis at the University of Zürich. The volume [a4] is a paean to the legacy of Gross. Reference [a4], Article by Keller–Künzi–Solèr, discusses the orthomodular axiom in depth, and contains a detailed proof of Solèr's theorem in the case where 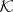 is commutative with the identity involution. Another proof of Solèr's theorem in the general case has been provided by A. Prestel [a6]. Solèr's theorem has applications to Baer
is commutative with the identity involution. Another proof of Solèr's theorem in the general case has been provided by A. Prestel [a6]. Solèr's theorem has applications to Baer  -rings, infinite-dimensional projective geometries, orthomodular lattices, and quantum logic [a2].
-rings, infinite-dimensional projective geometries, orthomodular lattices, and quantum logic [a2].
References
| [a1] | I. Amemiya, H. Araki, "A remark on Piron's paper" Publ. Res. Inst. Math. Sci. , A2 (1966/67) pp. 423–427 |
| [a2] | S.S. Holland Jr., "Orthomodularity in infinite dimensions: a theorem of M. Solèr" Bull. Amer. Math. Soc. , 32 (1995) pp. 205–234 |
| [a3] | H.A. Keller, "Ein nicht-klassischer Hilbertscher Raum" Math. Z. , 172 (1980) pp. 41–49 |
| [a4] | "Orthogonal geometry in infinite dimensional spaces" H.A. Keller (ed.) U.-M. Künzi (ed.) M. Wild (ed.) , Bayreuth. Math. Schrift. , 53 (1998) |
| [a5] | C. Piron, "Axiomatique quantique" Helv. Phys. Acta , 37 (1964) pp. 439–468 |
| [a6] | A. Prestel, "On Solèr's characterization of Hilbert spaces" Manuscripta Math. , 86 (1995) pp. 225–238 |
| [a7] | M.P. Solèr, "Characterization of Hilbert spaces with orthomodular spaces" Commun. Algebra , 23 (1995) pp. 219–243 |
| [a8] | W. John Wilbur, "On characterizing the standard quantum logics" Trans. Amer. Math. Soc. , 233 (1977) pp. 265–292 |
Solèr theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sol%C3%A8r_theorem&oldid=15459