Sahlqvist identities
The counterpart in the theory of Boolean algebras with operators of Sahlqvist formulas (cf. Sahlqvist theorem). Sahlqvist identities may be obtained from (modal) Sahlqvist formulas by viewing the latter as equations to be interpreted on Boolean algebras with operators (cf. Algebra of logic). For example, viewed algebraically, the (modal) Sahlqvist formula 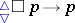 becomes
becomes  .
.
An explicit definition of Sahlqvist identities can be given as follows. Let 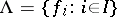 be a set of finitary (normal) additive operations. Let an untied term over
be a set of finitary (normal) additive operations. Let an untied term over 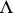 be a term that is either:
be a term that is either:
i) negative (in the sense that every variable occurs in the scope of an odd number of complementation signs  only);
only);
ii) of the form 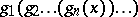 , where the
, where the  's are duals of unary operators in
's are duals of unary operators in 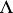 (i.e.,
(i.e., 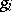 is defined by
is defined by 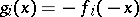 for some unary
for some unary 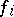 in
in 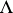 );
);
iii) closed (i.e., without occurrences of variables); or
iv) obtained from terms of type i), ii) or iii) by applying 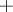 ,
,  and elements of
and elements of 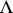 only.
only.
Then an identity is called a Sahlqvist identity if it is of the form  , where
, where  is obtained from complemented untied terms
is obtained from complemented untied terms 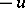 by applying duals of elements of
by applying duals of elements of 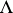 to terms that have no variables in common, and
to terms that have no variables in common, and  only. For example, the above inequality
only. For example, the above inequality  can be rewritten as
can be rewritten as 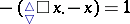 , which is of the required form. As a further example, all standard axioms for both relation and cylindric algebras can be brought to Sahlqvist form.
, which is of the required form. As a further example, all standard axioms for both relation and cylindric algebras can be brought to Sahlqvist form.
The canonical extension of a Boolean algebra with operators is the complete and atomic extension obtained from the Stone representation of the algebra. The important feature of Sahlqvist identities is that they are preserved in passing from a Boolean algebra with operators to its canonical extension; the corresponding result for modal logic is known as the Sahlqvist theorem, cf. [a5]. Identities with the latter property were first investigated in [a3].
References
| [a1] | R. Goldblatt, "Varieties of complex algebras" Ann. Pure and Applied Logic , 44 (1989) pp. 173–242 |
| [a2] | B. Jónsson, "On the canonicity of Sahlqvist identities" Studia Logica , 53 (1994) pp. 473–491 |
| [a3] | B. Jónsson, A. Tarski, "Boolean algebras with operators I" Amer. J. Math. , 73 (1951) pp. 891–939 |
| [a4] | M. de Rijke, Y. Venema, "Sahlqvist's theorem for Boolean algebras with operators, with an application to cylindric algebras" Studia Logica , 54 (1995) pp. 61–78 |
| [a5] | H. Sahlqvist, "Completeness and correspondence in the first and second order semantics for modal logic" S. Kanger (ed.) , Proc. Third Scand. Logic Symp. Uppsala (1973) , North-Holland (1975) pp. 110–143 |
Sahlqvist identities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sahlqvist_identities&oldid=18053