Runge domain
of the first kind
A domain 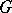 in the space
in the space 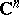 of complex variables
of complex variables 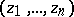 with the property that for any function
with the property that for any function 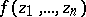 holomorphic in
holomorphic in  there exists a sequence of polynomials
there exists a sequence of polynomials
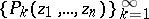 | (1) |
converging in  to
to 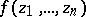 uniformly on every closed bounded set
uniformly on every closed bounded set  . The definition of a Runge domain of the second kind is obtained from the above by replacing the sequence (1) by a sequence of rational functions
. The definition of a Runge domain of the second kind is obtained from the above by replacing the sequence (1) by a sequence of rational functions 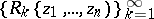 . For
. For 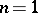 any simply-connected domain is a Runge domain of the first kind and any domain is a Runge domain of the second kind (see Runge theorem). For
any simply-connected domain is a Runge domain of the first kind and any domain is a Runge domain of the second kind (see Runge theorem). For  not all simply-connected domains are Runge domains and not all Runge domains are simply connected.
not all simply-connected domains are Runge domains and not all Runge domains are simply connected.
References
| [1] | B.A. Fuks, "Special chapters in the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [3] | G. Stolzenberg, "Polynomially and rationally convex sets" Acta Math. , 109 (1963) pp. 259–289 |
Comments
Two domains 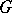 and
and 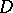 with
with  are called a Runge pair if every function holomorphic in
are called a Runge pair if every function holomorphic in 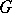 can be approximated uniformly on every compact subset of
can be approximated uniformly on every compact subset of 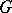 by functions holomorphic in
by functions holomorphic in  . One also says that
. One also says that 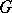 is (relatively) Runge in
is (relatively) Runge in  . To say that
. To say that 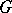 is a Runge domain (of the first kind) is equivalent to saying that
is a Runge domain (of the first kind) is equivalent to saying that 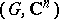 is a Runge pair.
is a Runge pair.
In addition there are the following generalizations: If 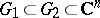 are two domains, then
are two domains, then 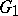 is called relatively Runge in
is called relatively Runge in 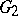 if every holomorphic function on
if every holomorphic function on 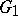 can be uniformly approximated on every compact subset of
can be uniformly approximated on every compact subset of 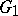 with holomorphic functions on
with holomorphic functions on 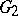 . Hence
. Hence 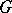 is a Runge domain of the first kind if and only if
is a Runge domain of the first kind if and only if  is relatively Runge in
is relatively Runge in 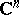 .
.
References
| [a1] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) |
| [a2] | J.E. Fornaess, B. Stensønes, "Lectures on counterexamples in several variables" , Princeton Univ. Press (1987) |
| [a3] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Sect. 4.5 |
Runge domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Runge_domain&oldid=12515