Riesz interpolation formula

A formula giving an expression for the derivative of a trigonometric polynomial at some point by the values of the polynomial itself at a finite number of points. If 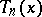is a trigonometric polynomial of degree with real coefficients, then for any real the following equality holds:

where , .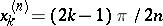

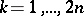Riesz' interpolation formula can be generalized to entire functions of exponential type: If 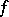is an entire function that is bounded on the real axis and of order 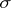, then

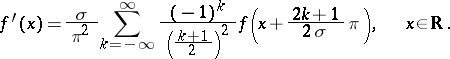Moreover, the series at right-hand side of the equality converges uniformly on the entire real axis.

This result was established by M. Riesz [1].

References

[1]	M. Riesz, "Formule d'interpolation pour la dérivée d'une polynôme trigonométrique" C.R. Acad. Sci. Paris , 158 (1914) pp. 1152–1154
[2]	S.N. Bernshtein, "Extremal properties of polynomials and best approximation of continuous functions of a real variable" , 1 , Moscow-Leningrad (1937) (In Russian)
[3]	S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)

References

[a1]	M. Riesz, "Eine trigonometrische Interpolationsformel und einige Ungleichungen für Polynome" Jahresber. Deutsch. Math.-Ver. , 23 (1914) pp. 354–368
[a2]	A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) pp. Chapt. 4 (Translated from Russian)
[a3]	A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) pp. Chapt. X