Residually-finite semi-group
finitely-approximable semi-group
A semi-group for any two distinct elements  and
and 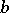 of which there is a homomorphism
of which there is a homomorphism 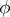 of it into a finite semi-group
of it into a finite semi-group 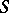 such that
such that 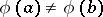 . The property of a semi-group
. The property of a semi-group 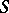 being residually finite is equivalent to that of
being residually finite is equivalent to that of 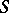 being a subdirect product of finite semi-groups. Residual finiteness is one of the more important finiteness conditions (see Semi-group with a finiteness condition); it is closely connected with algorithmic problems (cf. Algorithmic problem): if
being a subdirect product of finite semi-groups. Residual finiteness is one of the more important finiteness conditions (see Semi-group with a finiteness condition); it is closely connected with algorithmic problems (cf. Algorithmic problem): if 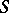 is a finitely-presented residually-finite semi-group, then there is an algorithm for solving the word problem in it. The residually-finite semi-groups include the free semi-groups, the free commutative semi-groups, the free nilpotent semi-groups of class
is a finitely-presented residually-finite semi-group, then there is an algorithm for solving the word problem in it. The residually-finite semi-groups include the free semi-groups, the free commutative semi-groups, the free nilpotent semi-groups of class  , the free inverse semi-groups (as algebras with two operations), the semi-lattices, the finitely-generated commutative semi-groups [1], the finitely-generated semi-groups of matrices over a nilpotent or commutative ring, and the finitely-generated regular semi-groups that are nilpotent of class
, the free inverse semi-groups (as algebras with two operations), the semi-lattices, the finitely-generated commutative semi-groups [1], the finitely-generated semi-groups of matrices over a nilpotent or commutative ring, and the finitely-generated regular semi-groups that are nilpotent of class  in the sense of Mal'tsev (see Nilpotent semi-group) [4]; see also Residually-finite group.
in the sense of Mal'tsev (see Nilpotent semi-group) [4]; see also Residually-finite group.
The direct product, the free product, the ordinal sum (see Band of semi-groups), and the  -direct union of an arbitrary set of residually-finite semi-groups are also residually-finite semi-groups. Other constructions do not, generally speaking, preserve residual finiteness. An ideal extension of a residually-finite semi-group
-direct union of an arbitrary set of residually-finite semi-groups are also residually-finite semi-groups. Other constructions do not, generally speaking, preserve residual finiteness. An ideal extension of a residually-finite semi-group 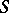 by an arbitrary residually-finite semi-group is residually-finite if, for example,
by an arbitrary residually-finite semi-group is residually-finite if, for example, 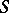 is reductive, that is, if any two distinct elements of
is reductive, that is, if any two distinct elements of 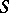 induce distinct left and distinct right inner translations; in particular, if
induce distinct left and distinct right inner translations; in particular, if 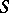 is a cancellation or inverse semi-group. The semi-lattice of a family of reductive residually-finite semi-groups is a residually-finite semi-group.
is a cancellation or inverse semi-group. The semi-lattice of a family of reductive residually-finite semi-groups is a residually-finite semi-group.
If 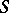 is a residually-finite semi-group, then all maximal subgroups of it are residually finite. For certain types of semi-groups this necessary condition is also sufficient; such as: regular semi-groups with a finite number of idempotents in every principal factor [2], Clifford inverse semi-groups, and completely
is a residually-finite semi-group, then all maximal subgroups of it are residually finite. For certain types of semi-groups this necessary condition is also sufficient; such as: regular semi-groups with a finite number of idempotents in every principal factor [2], Clifford inverse semi-groups, and completely  -simple semi-groups with a finite number of
-simple semi-groups with a finite number of 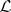 - or
- or 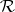 -classes (see Green equivalence relations). For a number of classes of semi-groups a characterization of the residually-finite semi-groups in them has been obtained in terms not using reduction to maximal subgroups.
-classes (see Green equivalence relations). For a number of classes of semi-groups a characterization of the residually-finite semi-groups in them has been obtained in terms not using reduction to maximal subgroups.
Varieties of residually-finite semi-groups have been characterized in several ways [3]. One such is the following. Let 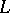 ,
, 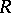 ,
, 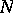 , and
, and 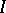 be, respectively, the two-element left zero and right zero semi-groups, the semi-group with zero multiplication, and a semi-lattice, let
be, respectively, the two-element left zero and right zero semi-groups, the semi-group with zero multiplication, and a semi-lattice, let 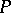 be the three-element semi-group
be the three-element semi-group 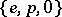 , where
, where 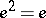 ,
, 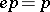 and the remaining products are equal to
and the remaining products are equal to  , and let
, and let 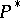 be the semi-group anti-isomorphic to
be the semi-group anti-isomorphic to 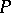 . A variety
. A variety 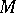 consists of residually-finite semi-groups if and only if
consists of residually-finite semi-groups if and only if 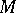 is generated by a subset of one of the following three sets:
is generated by a subset of one of the following three sets: 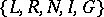 ,
, 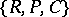 ,
, 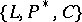 , where
, where 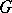 is a finite group with Abelian Sylow subgroups and
is a finite group with Abelian Sylow subgroups and  is a finite cyclic group.
is a finite cyclic group.
References
| [1] | A.I. Mal'tsev, "Homomorphisms onto finite groups" Uchen. Zap. Ivanovsk. Ped. Inst. , 18 (1958) pp. 49–60 (In Russian) |
| [2] | E.A. Golubov, "Finitely approximable regular semi-groups" Math. Notes , 17 : 3 (1975) pp. 247–251 Mat. Zam. , 17 : 3 (1975) pp. 423–432 |
| [3] | E.A. Golubov, M.V. Sapir, "Varieties of finitely approximable semigroups" Soviet Math. Dokl. , 20 : 4 (1979) pp. 828–832 Dokl. Akad. Nauk SSSR , 247 : 5 (1979) pp. 1037–1041 |
| [4] | G. Lallement, "On nilpotency and residual finiteness in semigroups" Pacific J. Math. , 42 : 3 (1972) pp. 693–700 |
Comments
References
| [a1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
Residually-finite semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Residually-finite_semi-group&oldid=14997