Replica
of an algebraic system 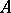 in a given class
in a given class 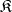 of algebraic systems of the same signature
of algebraic systems of the same signature
An algebraic system 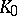 from
from 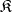 possessing the following properties: 1) there is a surjective homomorphism
possessing the following properties: 1) there is a surjective homomorphism 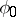 from
from 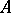 onto
onto  ; 2) if
; 2) if 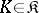 and if
and if 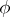 is a homomorphism from
is a homomorphism from 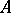 to
to 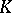 , then
, then 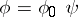 for some homomorphism
for some homomorphism 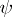 from the system
from the system 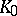 to
to 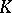 . The replica of the system
. The replica of the system 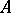 in the class
in the class 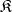 (if it exists) is uniquely defined up to an isomorphism. The class
(if it exists) is uniquely defined up to an isomorphism. The class 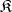 is called replica full if it contains a replica for any algebraic system of the same signature. A class of algebraic systems of a fixed signature is replica full if and only if it contains a one-element system and is closed with respect to taking subsystems and direct products. The axiomatizable replica-full classes (and only these) are quasi-varieties (cf. Quasi-variety).
is called replica full if it contains a replica for any algebraic system of the same signature. A class of algebraic systems of a fixed signature is replica full if and only if it contains a one-element system and is closed with respect to taking subsystems and direct products. The axiomatizable replica-full classes (and only these) are quasi-varieties (cf. Quasi-variety).
References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
Comments
The concept of a replica is closely related to that of a universal problem (cf. Universal problems).
A second notion of replica occurs in the theory of algebraic Lie algebras, the Lie algebras of algebraic subgroups of 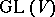 . Let
. Let 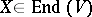 , where
, where 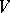 is a finite-dimensional vector space, and let
is a finite-dimensional vector space, and let  be the smallest algebraic Lie subalgebra of
be the smallest algebraic Lie subalgebra of 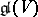 that contains
that contains  . The elements of
. The elements of 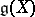 are called the replicas of
are called the replicas of 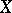 . One has that
. One has that 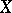 is nilpotent if and only if
is nilpotent if and only if  for all replicas
for all replicas 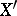 of
of 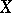 .
.
References
| [a1] | C. Chevalley, "Théorie des groupes de Lie" , 2 , Hermann (1951) pp. Chapt. II, §14 |
Replica. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Replica&oldid=15808