Remainder of a space

The set 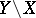 , where
, where 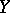 is a compactification of
is a compactification of 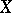 . The properties of a remainder depend strongly on those of
. The properties of a remainder depend strongly on those of 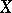 : A remainder is compact if and only if
: A remainder is compact if and only if 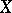 is locally compact; the existence of a zero-dimensional remainder depends broadly on whether
is locally compact; the existence of a zero-dimensional remainder depends broadly on whether 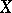 has the peripheral compactness property; if there exists a metrizable compactification of
has the peripheral compactness property; if there exists a metrizable compactification of 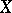 with remainder of dimension
with remainder of dimension 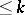 , then
, then 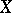 has an open base in which the intersection of the boundaries of any
has an open base in which the intersection of the boundaries of any 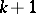 disjoint sets is compact; etc. If every connected compact subset of
disjoint sets is compact; etc. If every connected compact subset of 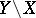 consists of a single point (for example, if
consists of a single point (for example, if 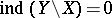 ), the remainder is said to be punctiform. If there exists at least one compactification with punctiform remainder, then one of these compactifications,
), the remainder is said to be punctiform. If there exists at least one compactification with punctiform remainder, then one of these compactifications, 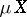 , is maximal, and, moreover, it is the minimal perfect extension of
, is maximal, and, moreover, it is the minimal perfect extension of  .
.
Comments
Some important properties, such as compactness, local compactness, paracompactness, the Lindelöf property, are possessed by all remainders of 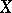 or by none. When the remainders of
or by none. When the remainders of 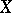 have such a property,
have such a property, 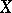 is said to have the property "at infinity" .
is said to have the property "at infinity" .
References
| [a1] | H.N. Inasaridze, "A generalization of perfect mappings" Soviet Math. Dokl. , 7 : 3 (1966) pp. 620–622 Dokl. Akad. Nauk SSSR , 168 (1966) pp. 266–268 |
Remainder of a space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Remainder_of_a_space&oldid=18941