Rayleigh equation

A non-linear ordinary differential equation of order two:

(*)

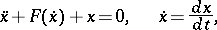where the function 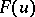satisfies the assumption:

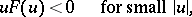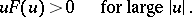The Rayleigh equation describes a typical non-linear system with one degree of freedom which admits auto-oscillations (cf. Auto-oscillation). This equation was named after Lord Rayleigh, who studied equations of this type related to problems in acoustics [1].

If one differentiates equation (*) and then puts 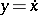, one obtains the Liénard equation

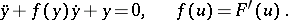The special case of the Rayleigh equation for

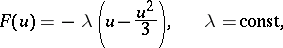is the van der Pol equation. Sometimes the following special case of equation (*) is called the Rayleigh equation:

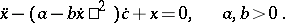There is a large number of studies concerned with the existence and uniqueness conditions for a limit cycle of the Rayleigh equation, that is, conditions under which auto-oscillations occur. The question of periodic solutions was studied also for different generalizations of the Rayleigh equation, e.g. for

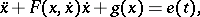where 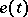is a periodic function.

The following equation is often called a Rayleigh-type system:

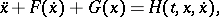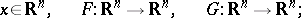moreover, it is usually assumed that

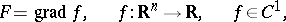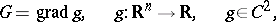and 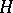is a bounded vector function that is periodic in 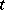. The problem of obtaining sufficient conditions for the existence of periodic solutions of such systems is of considerable interest.

See also the references to Liénard equation.

References

[1]	J.W. [Lord Rayleigh] Strutt, "Theory of sound" , 1 , Dover, reprint (1945)
[2]	L. Cesari, "Asymptotic behavior and stability problems in ordinary differential equations" , Springer (1959)

References

[a1]	J.J. Stoker, "Nonlinear vibrations in mechanical and electrical systems" , Interscience (1950)