Rank of an ordinary linear differential equation
in the complex domain,
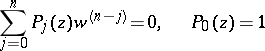 |
The number 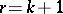 , where
, where
 |
if the coefficients in equation
are series which are convergent for large 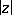 :
:
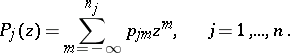 |
The concept of rank is used only when 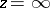 is a singular point of the differential equation . The rank of the differential equation is also called the rank of the singular point
is a singular point of the differential equation . The rank of the differential equation is also called the rank of the singular point 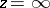 . If this point is a regular singular point, then
. If this point is a regular singular point, then  ; if it is an irregular singular point, then
; if it is an irregular singular point, then 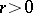 . The number
. The number  is called the subrank. The rank of the equation is an integer or a rational number. If the subrank is rational with denominator
is called the subrank. The rank of the equation is an integer or a rational number. If the subrank is rational with denominator 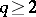 , then the subrank of the equation obtained from
, then the subrank of the equation obtained from
by the change of variable 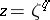 is an integer. The rank of the equation is invariant with respect to a change of variable of the form
is an integer. The rank of the equation is invariant with respect to a change of variable of the form 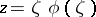 , with
, with 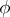 a holomorphic function at the point
a holomorphic function at the point  that is non-zero at this point.
that is non-zero at this point.
The concept of the rank of an equation is used in investigating the structure of the solutions to equation
with a singular point at infinity. Let 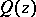 be a polynomial of degree
be a polynomial of degree 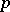 , let
, let
 |
be a formal series, and let 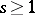 be an integer. The series
be an integer. The series
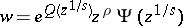 | (2) |
is a normal (subnormal, respectively) series of order 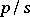 if
if 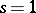 (
( , respectively). A solution to equation
, respectively). A solution to equation
which is represented by a normal (subnormal) series, convergent in a neighbourhood of  , is called a normal (subnormal) solution of the same order (see [2], [3]).
, is called a normal (subnormal) solution of the same order (see [2], [3]).
The order of a normal (subnormal) solution does not exceed the rank of the equation; this is true also for formal solutions of the form (2). If the rank  of equation
of equation
is an integer, then
has at least one formal solution of the form (2) of order  . The substitution
. The substitution 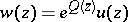 does not alter the rank of the equation. If the subrank is
does not alter the rank of the equation. If the subrank is 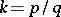 , where
, where  are mutually prime integers and
are mutually prime integers and  , then the equation has no less than
, then the equation has no less than 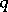 formal solutions of the form (2) of order
formal solutions of the form (2) of order  .
.
A Hamburger equation is an equation
with rational coefficients which has exactly two singular points: a regular one 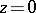 and an irregular one
and an irregular one  . For a Hamburger equation one can obtain sufficient conditions for it to have normal solutions; when
. For a Hamburger equation one can obtain sufficient conditions for it to have normal solutions; when 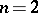 there are necessary and sufficient conditions for the existence of normal and subnormal solutions (see [2]).
there are necessary and sufficient conditions for the existence of normal and subnormal solutions (see [2]).
One also introduces the concept of rank in the case when equation
has a finite singular point (see [2], [3]).
In the case of a linear system of  ordinary differential equations in the complex domain,
ordinary differential equations in the complex domain,
 | (3) |
where 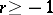 is an integer and the matrix-function
is an integer and the matrix-function 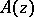 is holomorphic at
is holomorphic at 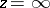 and
and  , the number
, the number 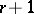 is called the rank of the system (3) or the rank of the singular point
is called the rank of the system (3) or the rank of the singular point 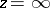 , the number
, the number  is its subrank (see [4]–[6]). If
is its subrank (see [4]–[6]). If 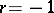 , then the point
, then the point 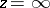 is a regular singular point; in contrast to a scalar equation , the point
is a regular singular point; in contrast to a scalar equation , the point 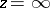 can be a regular singular point if
can be a regular singular point if 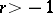 (see [4]).
(see [4]).
References
| [1] | H. Poincaré, "Sur les intégrales irregulières des équations linéaires" Acta Math. , 8 (1866) pp. 295–344 |
| [2] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
| [3] | K.Ya. Latysheva, N.I. Tereshchenko, G.S. Orel, "Normally regular solutions and their applications" , Kiev (1974) (In Russian) |
| [4] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
| [5] | E. Kamke, "Handbuch der gewöhnliche Differentialgleichungen" , Chelsea, reprint (1947) |
| [6] | W. Wasov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
Comments
For the word rank sometimes the term grade is used. The following can be proved, see [a1]. For every  a solution
a solution 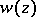 exists for which
exists for which
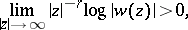 |
except for a finite number of directions.
References
| [a1] | E. Hille, "Lectures on ordinary differential equations" , Addison-Wesley (1969) |
Rank of an ordinary linear differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rank_of_an_ordinary_linear_differential_equation&oldid=16416