Peano derivative
One of the generalizations of the concept of a derivative. Let there exist a 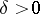 such that for all
such that for all  with
with 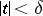 one has
one has
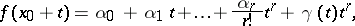 |
where  are constants and
are constants and 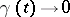 as
as 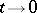 ; let
; let 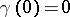 . Then
. Then  is called the generalized Peano derivative of order
is called the generalized Peano derivative of order  of the function
of the function 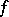 at the point
at the point 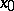 . Symbol:
. Symbol: 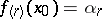 ; in particular,
; in particular, 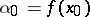 ,
, 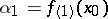 . If
. If 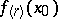 exists, then
exists, then 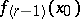 ,
, 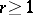 , also exists. If the finite ordinary two-sided derivative
, also exists. If the finite ordinary two-sided derivative 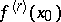 exists, then
exists, then 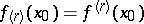 . The converse is false for
. The converse is false for 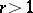 : For the function
: For the function
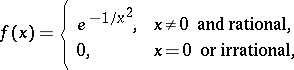 |
one has 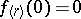 ,
, 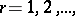 but
but 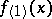 does not exist for
does not exist for 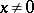 (since
(since 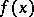 is discontinuous for
is discontinuous for 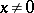 ). Consequently, the ordinary derivative
). Consequently, the ordinary derivative 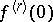 does not exist for
does not exist for 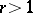 .
.
Infinite generalized Peano derivatives have also been introduced. Let for all 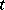 with
with 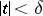 ,
,
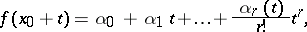 |
where  are constants and
are constants and 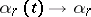 as
as 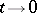 (
(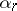 is a number or the symbol
is a number or the symbol 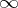 ). Then
). Then 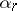 is also called the Peano derivative of order
is also called the Peano derivative of order  of the function
of the function 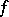 at the point
at the point 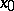 . It was introduced by G. Peano.
. It was introduced by G. Peano.
Peano derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Peano_derivative&oldid=12168