Parametric integral-representation method
A method in the geometric theory of functions of a complex variable that is used to solve extremal problems in function classes by representing these classes using integrals depending on parameters.
Among these classes are the Carathéodory class, the class of univalent star-like functions in the disc, and the class of typically-real functions (cf. Star-like function and Typically-real function). The functions of these classes have parametric representations involving a Stieltjes integral
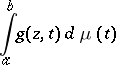 |
with given real numbers  and
and 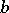 , and a function
, and a function  (the kernel of the class),
(the kernel of the class), 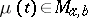 , where
, where 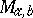 is the class of non-decreasing functions on
is the class of non-decreasing functions on 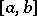 ,
,  (
(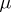 is the parameter of the class).
is the parameter of the class).
For classes of functions having a parametric representation by Stieltjes integrals, variational formulas have been obtained that show, in the solution of extremal problems in these classes, that the extremal function is of the form
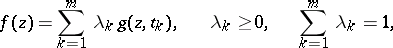 |
where 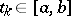 , and the value of
, and the value of 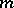 is known (see [1], Chapt. 11, [3]).
is known (see [1], Chapt. 11, [3]).
To find the ranges of functionals and systems of functionals on such classes the following theorems are sometimes useful.
1) The set 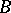 of points
of points 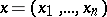 of the
of the  -dimensional Euclidean space
-dimensional Euclidean space 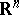 admitting a representation
admitting a representation
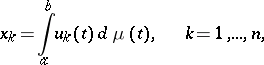 |
where the 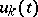 are fixed continuous real-valued functions on
are fixed continuous real-valued functions on  and
and 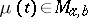 coincides with the closed convex hull
coincides with the closed convex hull  of the set
of the set  of the points
of the points
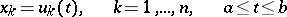 |
(a theorem of Riesz).
2) Every point 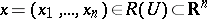 can be represented in the form
can be represented in the form
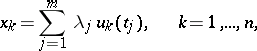 |
where  ,
, 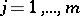 ,
, 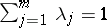 ,
, 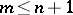 , and if
, and if 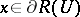 , then
, then 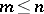 (a theorem of Carathéodory).
(a theorem of Carathéodory).
3) There exists at least one non-decreasing function 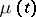 ,
,  , such that
, such that
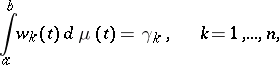 |
where
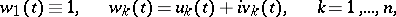 |
 ,
,  are given real-valued continuous functions on
are given real-valued continuous functions on 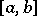 ,
, 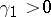 , and
, and 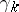 are given complex numbers, if and only if whenever the complex numbers
are given complex numbers, if and only if whenever the complex numbers  satisfy
satisfy
 |
then also
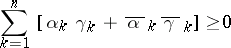 |
(a theorem of Riesz).
These theorems make it possible to give geometric and algebraic characterizations of the ranges of systems of coefficients and individual coefficients on classes of functions that are regular and have positive real part in the disc (or an annulus), or are regular and typically real in the disc (or annulus), and on some other classes (see [1], Appendix; [4], ).
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | M.G. Krein, "The ideas of P.L. Chebyshev and A.A. Markov in the theory of limiting values of integrals, and their further development" Uspekhi Mat. Nauk , 6 : 4 (1951) pp. 3–120 (In Russian) |
| [3] | N.A. Lebedev, I.A. Aleksandrov, "On the variational method in classes of functions representable by means of Stieltjes integrals" Proc. Steklov Inst. Math. , 94 (1968) pp. 91–103 Trudy Mat. Inst. Steklov. , 94 (1968) pp. 79–89 |
| [4] | E.G. Goluzina, "The value domains of the coefficient systems of a certain class of functions meromorphic in a disk" Proc. Steklov Inst. Math. , 94 (1968) pp. 37–52 Trudy Mat. Inst. Steklov. , 94 (1968) pp. 33–46 |
| [5a] | E.G. Goluzina, "On domains of values of systems of functionals in some classes of functions, representable by a Stieltjes integral" J. Soviet Math. , 2 : 6 (1974) pp. 582–605 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. , 24 (1972) pp. 29–62 |
| [5b] | E.G. Goluzina, "Ranges of values of systems of coefficients in the class of functions with positive real part in an annulus" J. Soviet Math. , 8 : 6 (1977) pp. 642–661 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. , 44 (1972) pp. 17–40 |
| [5c] | E.G. Goluzina, "Ranges of certain systems of functionals in classes of functions with a positive real part" J. Soviet Math. , 19 : 6 (1982) pp. 1630–1636 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. , 100 (1980) pp. 17–25 |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11 |
Parametric integral-representation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parametric_integral-representation_method&oldid=13001