Orthogonal polynomials on a complex domain
The general name for polynomials orthogonal on the circle, over a contour or over an area. Unlike the case of orthogonality in a real domain, the polynomials of the three kinds of systems mentioned can have imaginary coefficients and are examined for all complex values of the independent variable. A characteristic feature of cases of orthogonality on a complex domain is that analytic functions of a complex variable which satisfy certain supplementary conditions in a neighbourhood of the boundary of the domain of analyticity can usually be expanded in a Fourier series in these systems (cf. Fourier series in orthogonal polynomials).
Orthogonal polynomials on the circle.
A system of polynomials 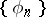 having positive leading coefficient and satisfying the orthogonality (usually orthonormality) condition:
having positive leading coefficient and satisfying the orthogonality (usually orthonormality) condition:
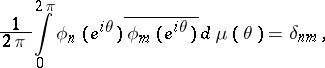 |
where 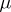 is a bounded non-decreasing function on the interval
is a bounded non-decreasing function on the interval 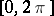 with an infinite number of points of growth, called a distribution function, while
with an infinite number of points of growth, called a distribution function, while 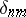 is the Kronecker symbol. A recurrence relation and the analogue of the Christoffel–Darboux formula holds for the polynomials
is the Kronecker symbol. A recurrence relation and the analogue of the Christoffel–Darboux formula holds for the polynomials 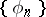 , in the same way as in the case of orthogonality on an interval.
, in the same way as in the case of orthogonality on an interval.
Asymptotic properties are examined under the condition
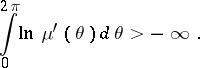 |
The case of orthogonality on the circle as a periodic case has been studied in sufficient detail, and the results of the approximation of periodic functions by trigonometric polynomials have been successfully used.
Let the polynomials 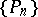 be orthonormal on the segment
be orthonormal on the segment 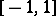 with differential weight function
with differential weight function 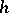 , and let the weight function on the circle have the form
, and let the weight function on the circle have the form
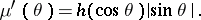 |
Under the condition 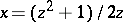 , the Szegö formula
, the Szegö formula
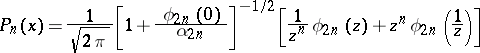 |
holds, where 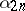 is the leading coefficient of the polynomial
is the leading coefficient of the polynomial 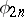 .
.
If an analytic function 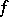 in the disc
in the disc 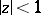 has non-tangential boundary values on the circle
has non-tangential boundary values on the circle  , then under certain supplementary conditions the expansion
, then under certain supplementary conditions the expansion
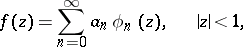 | (1) |
holds; its coefficients are defined by the formula
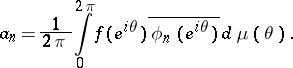 |
Series of the form (1) are direct generalizations of Taylor series: if 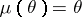 ,
, 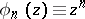 . Given certain conditions on the distribution function
. Given certain conditions on the distribution function 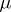 , the series (1) converges or diverges simultaneously with the Taylor series of the same function
, the series (1) converges or diverges simultaneously with the Taylor series of the same function 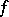 at the points of the circle
at the points of the circle  , i.e. the theorem on equiconvergence of these two series holds.
, i.e. the theorem on equiconvergence of these two series holds.
Orthogonal polynomials over a contour.
A system of polynomials 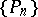 having positive leading coefficient and satisfying the condition
having positive leading coefficient and satisfying the condition
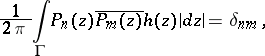 |
where 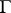 is a rectifiable Jordan curve (usually closed) in the complex plane, while the weight function
is a rectifiable Jordan curve (usually closed) in the complex plane, while the weight function 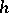 is Lebesgue integrable and positive almost-everywhere on
is Lebesgue integrable and positive almost-everywhere on 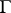 .
.
Let, in the simply-connected bounded domain 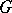 bounded by the curve
bounded by the curve 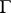 , an analytic function
, an analytic function 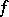 be given whose boundary values on the contour
be given whose boundary values on the contour 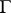 are square integrable with respect to the weight function
are square integrable with respect to the weight function 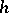 . Using the formula for the coefficients,
. Using the formula for the coefficients,
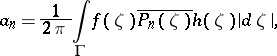 |
a Fourier series in the orthogonal polynomials,
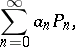 | (2) |
then corresponds to this function. These series are a natural generalization of Taylor series with respect to the orthogonality property in the case of a simply-connected domain, and serve as a representation of analytic functions. If the completeness condition
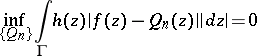 |
is fulfilled, where the infimum is taken over the set of all polynomials 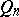 , then the series (2) converges in the mean to the function
, then the series (2) converges in the mean to the function 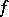 along the contour
along the contour 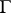 with weight
with weight 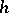 and, under certain supplementary conditions, inside the domain
and, under certain supplementary conditions, inside the domain 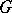 as well.
as well.
Orthogonal polynomials over a domain.
A system of polynomials 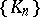 having positive leading coefficient and satisfying the condition
having positive leading coefficient and satisfying the condition
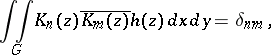 |
where the weight function 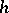 is non-negative, integrable with respect to the area of a bounded domain
is non-negative, integrable with respect to the area of a bounded domain 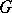 , and not equal to zero. If the completeness condition
, and not equal to zero. If the completeness condition
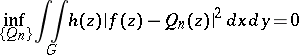 |
is fulfilled, where the infimum is taken over the set of all polynomials 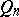 , then the Fourier series in the polynomials
, then the Fourier series in the polynomials 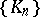 of an analytic function
of an analytic function 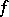 in a simply-connected domain
in a simply-connected domain 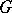 converges in the mean (with respect to the area of the domain
converges in the mean (with respect to the area of the domain 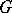 ) with weight
) with weight 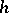 to this function
to this function 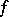 and, under certain supplementary conditions, inside the domain
and, under certain supplementary conditions, inside the domain 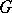 as well.
as well.
References
| [1a] | G. Szegö, "Beiträge zur Theorie der Toeplitzschen Formen, I" Math. Z. , 6 (1920) pp. 167–202 (Also: Collected Works, Vol. 1, Birkhäuser, 1982, pp. 237–272) |
| [1b] | G. Szegö, "Beiträge zur Theorie der Toeplitzschen Formen, II" Math. Z. , 9 (1921) pp. 167–190 (Also: Collected Works, Vol. 1, Birkhäuser, 1982, pp. 279–305) |
| [1c] | G. Szegö, "Über orthogonale Polynome, die zu einer gegebenen Kurve der komplexen Ebene gehören" Math. Z. , 9 (1921) pp. 218–270 (Also: Collected Works, Vol. 1, Birkhäuser, 1982, pp. 316–368) |
| [2] | T. Carleman, "Über die Approximation analytischer Funktionen durch lineare Aggregate von vorgegebenen Potenzen" Ark. for Mat., Astr. och Fys. , 17 : 9 (1922–1923) pp. 1–30 |
| [3] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
| [4] | Ya.L. Geronimus, "Polynomials orthogonal on a circle and interval" , Pergamon (1960) (Translated from Russian) |
| [5] | V.I. Smirnov, "On the theory of orthogonal polynomials of a complex variable" Zh. Leningrad. Fiz.-Mat. Obshch. , 2 : 1 (1928) pp. 155–179 (In Russian) |
| [6] | P.P. Korovkin, "On polynomials orthogonal on a rectifiable contour in the presence of a weight" Mat. Sb. , 9 : 3 (1941) pp. 469–485 (In Russian) |
| [7] | P.K. Suetin, "Fundamental properties of polynomials orthogonal on a contour" Russian Math.Surveys , 21 : 2 (1966) pp. 35–83 Uspekhi Mat. Nauk , 21 : 2 (1966) pp. 41–88 |
| [8] | P.K. Suetin, "Polynomials orthogonal over a region and Bieberbach polynomials" Proc. Steklov Inst. Math. , 100 (1974) Trudy Mat. Inst. Steklov. , 100 (1971) |
Comments
See also the state-of-the-art paper [a2] (on the theory) and [a1] (on digital signal processing applications).
References
| [a1] | Ph. Delsarte, Y. Genin, "On the role of orthogonal polynomials on the unit circle in digital signal processing applications" P. Nevai (ed.) , Orthogonal polynomials: theory and practice , Kluwer (1990) pp. 115–133 |
| [a2] | E.B. Saff, "Orthogonal polynomials from a complex perspective" P. Nevai (ed.) , Orthogonal polynomials: theory and practice , Kluwer (1990) pp. 363–393 |
Orthogonal polynomials on a complex domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_polynomials_on_a_complex_domain&oldid=16077