Net (in differential geometry)
A system 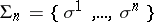 of
of  families
families 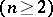 of sufficiently smooth curves in a domain
of sufficiently smooth curves in a domain 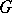 of an
of an  -dimensional differentiable manifold
-dimensional differentiable manifold 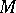 such that: 1) through each point
such that: 1) through each point 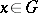 there passes exactly one curve of each family
there passes exactly one curve of each family 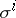 ; and 2) the tangent vectors to these curves at
; and 2) the tangent vectors to these curves at  form a basis for the tangent space
form a basis for the tangent space 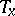 to
to 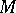 at
at  . The tangent vectors to the curves of one family
. The tangent vectors to the curves of one family 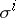 belong to a
belong to a 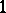 -dimensional distribution
-dimensional distribution 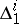 defined in
defined in 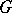 . The conditions for a family of curves to form a net in a certain neighbourhood of a point need not hold when the curves are extended. The curves of
. The conditions for a family of curves to form a net in a certain neighbourhood of a point need not hold when the curves are extended. The curves of 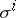 are the integral curves of
are the integral curves of 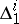 . A net
. A net 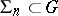 is defined by specifying
is defined by specifying  one-dimensional distributions
one-dimensional distributions 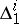 such that the tangent space
such that the tangent space 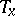 at each
at each 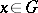 is the direct sum of the subspaces
is the direct sum of the subspaces 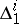 ,
, 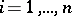 . A net
. A net 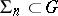 defines in
defines in 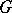
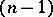 -dimensional distributions
-dimensional distributions 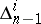 such that at each point
such that at each point 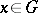 the subspace
the subspace 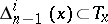 is the direct sum of the
is the direct sum of the 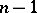 one-dimensional subspaces
one-dimensional subspaces 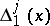 ,
, 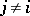 . The following types of nets are distinguished: holonomic nets, partially holonomic nets, for which certain of the
. The following types of nets are distinguished: holonomic nets, partially holonomic nets, for which certain of the 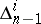 are integrable and the remainder are not (such nets are distinguished according to the number of non-integrable distributions), and non-holonomic nets, for which all
are integrable and the remainder are not (such nets are distinguished according to the number of non-integrable distributions), and non-holonomic nets, for which all 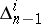 are non-integrable.
are non-integrable.
If a distribution 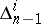 ,
, 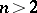 , is integrable and
, is integrable and 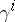 is an integral curve of
is an integral curve of 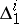 , then through each point
, then through each point 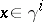 there passes an integral manifold of
there passes an integral manifold of 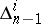 that carries a net
that carries a net 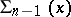 of curves belonging to the families
of curves belonging to the families 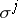 ,
, 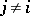 .
.
A net 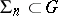 can also be defined by one of the following means: a) by a system of vector fields
can also be defined by one of the following means: a) by a system of vector fields 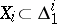 ; b) by a system of differential
; b) by a system of differential 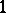 -forms
-forms 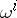 such that
such that 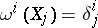 ; or c) by the field of an affinor
; or c) by the field of an affinor 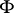 such that
such that 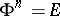 (
(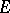 is the identity affinor).
is the identity affinor).
In the study of nets there are three basic problems: the intrinsic properties of nets, the exterior properties and an investigation of diffeomorphisms of nets.
The intrinsic properties of nets are induced by the structure of the manifold that carries the net. For example, a net 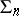 in a space
in a space 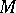 with an affine connection
with an affine connection  is called geodesic if all its curves are geodesic. If a Riemannian manifold
is called geodesic if all its curves are geodesic. If a Riemannian manifold 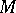 with a torsion-free connection in which the metric tensor is covariantly constant carries an orthogonal Chebyshev net of the first kind, then
with a torsion-free connection in which the metric tensor is covariantly constant carries an orthogonal Chebyshev net of the first kind, then 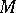 is locally Euclidean. The connection of such nets with parallel transfer of vectors on a surface was established by L. Bianchi (1922). This connection is at the basis of A.P. Norden's definition of a Chebyshev net of the first kind in a space with an affine connection.
is locally Euclidean. The connection of such nets with parallel transfer of vectors on a surface was established by L. Bianchi (1922). This connection is at the basis of A.P. Norden's definition of a Chebyshev net of the first kind in a space with an affine connection.
The exterior properties of a net are induced by the structure of the ambient space 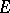 . For example, suppose that a net
. For example, suppose that a net 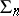 defined in a domain
defined in a domain 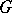 on a smooth surface
on a smooth surface 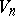 in
in 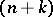 -dimensional projective space
-dimensional projective space 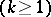 is conjugate, that is, at each point
is conjugate, that is, at each point 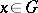 the directions
the directions 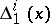 ,
, 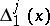 of the tangents to any two curves of
of the tangents to any two curves of 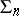 through
through  are conjugate (two directions are conjugate if each belongs to the characteristic of the tangent plane
are conjugate (two directions are conjugate if each belongs to the characteristic of the tangent plane  when it is displaced in the other direction). If
when it is displaced in the other direction). If 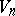 is not contained in a projective space of dimension less than
is not contained in a projective space of dimension less than 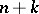 , then for
, then for 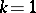 ,
, 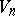 carries an infinite set of conjugate nets; for
carries an infinite set of conjugate nets; for 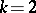 the surface carries, in general, a unique conjugate net, but there are
the surface carries, in general, a unique conjugate net, but there are  -dimensional surfaces on which there are no conjugate nets; for
-dimensional surfaces on which there are no conjugate nets; for 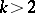 only
only  -dimensional surfaces of a special structure carry a conjugate net. For
-dimensional surfaces of a special structure carry a conjugate net. For 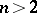 a conjugate net need not be holonomic (see [3]). A special case of a holonomic conjugate net is an
a conjugate net need not be holonomic (see [3]). A special case of a holonomic conjugate net is an  -conjugate system: A net
-conjugate system: A net 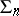 with the property that the tangents to the curves of each family taken along any curve of any other family form a developable surface. Conjugate systems exist in a projective space of any dimension
with the property that the tangents to the curves of each family taken along any curve of any other family form a developable surface. Conjugate systems exist in a projective space of any dimension 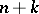 for
for 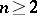 ,
, 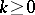 . Surfaces
. Surfaces 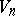 that carry an
that carry an  -conjugate system in the
-conjugate system in the 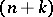 -dimensional projective space, when
-dimensional projective space, when 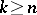 , and for which at each point
, and for which at each point 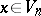 the osculating space (the space of second differentials of the point
the osculating space (the space of second differentials of the point  ) has dimension
) has dimension 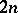 , were first considered by E. Cartan [4] under the name "manifolds of special projective type" (Cartan surfaces). The concept of the Laplace transformation (in geometry) was extended to such nets (see [5], [6]).
, were first considered by E. Cartan [4] under the name "manifolds of special projective type" (Cartan surfaces). The concept of the Laplace transformation (in geometry) was extended to such nets (see [5], [6]).
In the study of diffeomorphisms of nets, in terms of known properties of a net 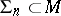 one describes properties of the net
one describes properties of the net 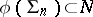 for a given diffeomorphism
for a given diffeomorphism 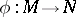 (for example, under a bending deformation or under a conformal mapping of a surface carrying a net), or one looks for a diffeomorphism
(for example, under a bending deformation or under a conformal mapping of a surface carrying a net), or one looks for a diffeomorphism 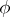 that preserves certain properties of
that preserves certain properties of 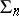 . For example, a net
. For example, a net 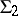 on a surface in Euclidean space is called a rhombic net (a conformal Chebyshev net) if it admits a conformal mapping onto a Chebyshev net. On every surface of revolution the asymptotic net is rhombic.
on a surface in Euclidean space is called a rhombic net (a conformal Chebyshev net) if it admits a conformal mapping onto a Chebyshev net. On every surface of revolution the asymptotic net is rhombic.
References
| [1] | A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian) |
| [2] | Ya.S. Dubnov, S.A. [S.A. Fuks] Fuchs, "Sur quelques réseaux de l'espace analogues au réseau de Tchebychev" Dokl. Akad. Nauk SSSR , 28 : 2 (1940) pp. 102–105 |
| [3] | V.T. Bazylev, "Multidimensional nets and their transformations" Itogi Nauk. Geom. 1963 (1965) pp. 138–164 (In Russian) |
| [4] | E. Cartan, "Sur les variétés de courbure constante d'un espace euclidien ou non euclidien" Bull. Soc. Math. France , 47 (1919) pp. 125–160 |
| [5] | S.S. Chern, "Laplace transforms of a class of higher dimensional varieties in a projective space of  dimensions" Proc. Nat. Acad. Sci. USA , 30 (1944) pp. 95–97 dimensions" Proc. Nat. Acad. Sci. USA , 30 (1944) pp. 95–97 |
| [6] | R.V. Smirnov, "Laplace transforms of  conjugate systems" Dokl. Akad. Nauk SSSR , 71 : 3 (1950) pp. 437–439 (In Russian) conjugate systems" Dokl. Akad. Nauk SSSR , 71 : 3 (1950) pp. 437–439 (In Russian) |
Net (in differential geometry). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Net_(in_differential_geometry)&oldid=16921