Multi-operator group
group with multiple operators,  -group
-group
A universal algebra which is a group relative to the addition operation 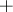 (which need not be commutative) and in which there is given a system of operations
(which need not be commutative) and in which there is given a system of operations  of arity
of arity 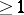 . It is assumed that the zero element
. It is assumed that the zero element  of the additive group
of the additive group 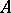 is a subalgebra, that is,
is a subalgebra, that is, 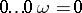 for all
for all 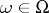 . Thus, a multi-operator group combines the concepts of a group, a linear algebra and a ring. An ideal of an
. Thus, a multi-operator group combines the concepts of a group, a linear algebra and a ring. An ideal of an  -group is a normal subgroup
-group is a normal subgroup 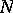 of
of 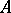 such that
such that
 |
for all  ,
, 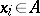 ,
, 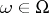 ,
, 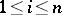 . Congruences on a multi-operator group are described by coset classes relative to ideals.
. Congruences on a multi-operator group are described by coset classes relative to ideals.
Let  ,
,  and
and  be
be  -subgroups in an
-subgroups in an  -group
-group 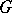 (that is, subalgebras of the universal algebra
(that is, subalgebras of the universal algebra 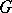 ), where
), where 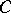 is generated by
is generated by 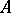 and
and 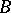 . The mutual commutator
. The mutual commutator 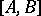 of the subgroups
of the subgroups 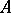 and
and  is the ideal in
is the ideal in 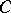 generated by all elements of the form
generated by all elements of the form
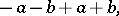 |
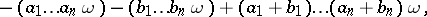 |
where 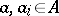 ,
, 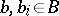 ,
, 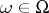 . Let
. Let 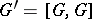 . A multi-operator group
. A multi-operator group 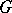 is called Abelian if
is called Abelian if 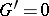 . Inductively one defines ideals
. Inductively one defines ideals 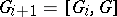 , where
, where 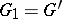 , and
, and  , where
, where 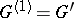 . A multi-operator group
. A multi-operator group 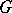 is called nilpotent if
is called nilpotent if 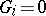 , and solvable if
, and solvable if 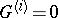 for some
for some 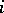 . Many of the properties of the corresponding classes of groups and rings can be transferred to these classes of multi-operator groups. A multi-operator group
. Many of the properties of the corresponding classes of groups and rings can be transferred to these classes of multi-operator groups. A multi-operator group 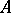 is called a multi-operator (linear)
is called a multi-operator (linear)  -algebra over a commutative associative ring
-algebra over a commutative associative ring 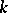 with an identity if the addition in
with an identity if the addition in 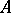 is commutative, if
is commutative, if 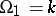 , where
, where  is the set of unary operations from
is the set of unary operations from  , and if all operations from
, and if all operations from  are semi-linear over
are semi-linear over  (see [2]–[6], and Semi-linear mapping).
(see [2]–[6], and Semi-linear mapping).
References
| [1] | P.J. Higgins, "Groups with multiple operators" Proc. London Math. Soc. , 6 (1956) pp. 366–416 |
| [2] | A.G. Kurosh, "Free sums of multi-operator algebras" Sibirsk. Mat. Zh. , 1 : 1 (1960) pp. 62–70 (In Russian) |
| [3] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [4] | A.G. Kurosh, "General algebra. Lectures for the academic year 1969/70" , Moscow (1974) (In Russian) |
| [5] | A.G. Kurosh, "Multioperator rings and algebras" Russian Math. Surveys , 24 : 1 (1969) pp. 1–13 Uspekhi Mat. Nauk. , 24 : 1 (1969) pp. 3–15 |
| [6] | T.M. Baranovich, M.S. Burgin, "Linear  -algebras" Russian Math. Surveys , 30 : 4 (1975) pp. 65–113 Uspekhi Mat. Nauk. , 30 : 4 (1975) pp. 61–106 -algebras" Russian Math. Surveys , 30 : 4 (1975) pp. 65–113 Uspekhi Mat. Nauk. , 30 : 4 (1975) pp. 61–106 |
| [7] | V.A. Artamonov, "Universal algebras" Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 14 (1976) pp. 191–248 (In Russian) |
| [8] | , Rings , 1 , Novosibirsk (1973) pp. 41–45 |
Multi-operator group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-operator_group&oldid=18026