Monogeneity set

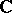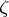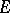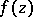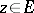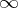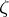The set of all derived numbers (Dini derivatives, cf. Dini derivative) of a given function of a complex variable at a given point. More precisely, let be a set in the complex plane , let be a non-isolated point of and let be a complex function of . A complex number (proper or equal to ) is called a derived number (or Dini derivative) of at relative to 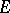if there is a sequence 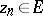with the properties: , ,

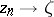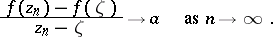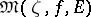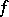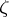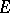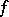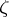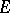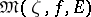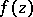The set of all derived numbers of at relative to is called the monogeneity set of at relative to (see [1]). The set consists of a unique finite point if and only if is a monogenic function at 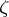relative to 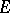and . The set 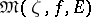is always closed, and for each closed set 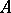in the extended complex plane 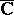, each set 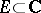and each finite non-isolated point 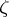of 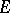, there is a function 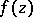, , such that 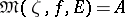. If 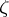is an interior point of 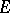, then for any function 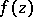that is continuous in a neighbourhood of 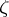, the set is closed and connected (a continuum) in 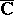and, conversely, for any continuum 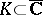there is a function 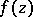, continuous in a neighbourhood of 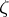, for which . If 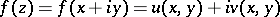is differentiable with respect to the set of real variables 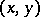at an interior point 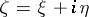of 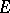, then 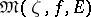is the circle 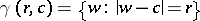(possibly degenerating into a point, 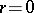) with centre 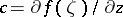and radius 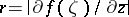, where

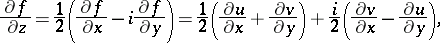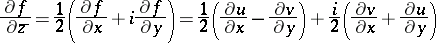are the so-called formal derivatives. The converse is also true: Each circle is the monogeneity set for some function 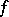, differentiable with respect to 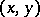, at a given interior point 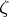of .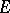

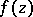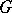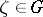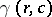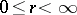If is continuous in a domain , then at almost every the set is either a circle , , or is 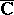(see [2]). In the general case of an arbitrary (not necessarily measurable) set 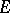and an arbitrary (not necessarily measurable) finite function 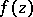, , 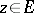at almost every point one of the following three cases holds: a) 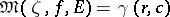, , 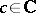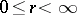; b) 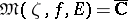; or c) 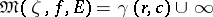, , 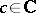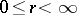. Here, a) holds at almost every differentiability point of 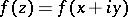with respect to 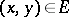and one of the first two cases holds at almost every continuity point of 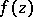. Each of the cases a)–c) may be realized individually at almost every point .

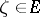For some natural generalizations to the multi-dimensional case see [4].

References

[1]	V.S. Fedorov, "The work of N.N. Luzin on the theory of functions of a complex variable" Uspekhi Mat. Nauk , 7 : 2 (1952) pp. 7–16 (In Russian)
[2]	Yu.Yu. Trokhimchuk, "Continuous mappings and monogeneity conditions" , Moscow (1963) (In Russian)
[3]	E.P. Dolzhenko, "On the derived numbers of complex functions" Izv. Akad. Nauk SSSR Ser. Mat. , 26 (1962) pp. 347–360 (In Russian)
[4]	A.V. Bondar, "Continuous operator conformal mappings" Ukr. Math. J. , 32 : 3 (1980) pp. 207–212 Ukrain. Mat. Zh. , 32 : 3 (1980) pp. 314–322