Minimax property
of eigen values
A special type of relationship connecting the eigen values of a completely-continuous self-adjoint operator 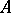 (cf. also Completely-continuous operator) with the maximum and minimum values of the associated quadratic form
(cf. also Completely-continuous operator) with the maximum and minimum values of the associated quadratic form 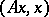 . Let
. Let 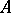 be a completely-continuous self-adjoint operator on a Hilbert space
be a completely-continuous self-adjoint operator on a Hilbert space  . The spectrum of
. The spectrum of 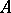 consists of a finite or countable set of real eigen values
consists of a finite or countable set of real eigen values 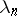 having unique limit point zero. The root subspaces corresponding to the non-zero eigen values consist of eigen vectors and are finite dimensional; the eigen subspaces associated with distinct eigen values are mutually orthogonal;
having unique limit point zero. The root subspaces corresponding to the non-zero eigen values consist of eigen vectors and are finite dimensional; the eigen subspaces associated with distinct eigen values are mutually orthogonal;  has a complete system of eigen vectors. The spectral decomposition of
has a complete system of eigen vectors. The spectral decomposition of 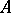 (cf. Spectral decomposition of a linear operator) has the form:
(cf. Spectral decomposition of a linear operator) has the form: 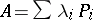 , where
, where  are the distinct eigen values,
are the distinct eigen values, 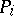 are the projection operators onto the corresponding eigen spaces, and the series converges in the operator norm. The norm of
are the projection operators onto the corresponding eigen spaces, and the series converges in the operator norm. The norm of 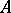 coincides with the maximum modulus of the eigen values and with
coincides with the maximum modulus of the eigen values and with 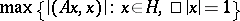 ; the maximum is attained at the corresponding eigen vector.
; the maximum is attained at the corresponding eigen vector.
Let 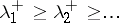 be the positive eigen values of
be the positive eigen values of 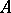 , where each eigen value is repeated as often as its multiplicity. Then
, where each eigen value is repeated as often as its multiplicity. Then
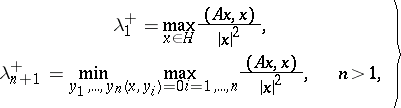 | (1) |
where 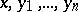 are arbitrary non-zero vectors in
are arbitrary non-zero vectors in 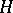 . Similar relations hold for the negative eigen values
. Similar relations hold for the negative eigen values 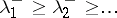 :
:
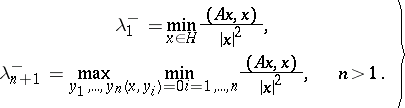 | (2) |
Relations (1) and (2) are applied for finding the eigen values of integral operators with a symmetric kernel. If 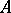 and
and 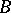 are completely-continuous self-adjoint operators,
are completely-continuous self-adjoint operators, 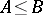 (that is,
(that is, 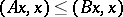 ),
),  and
and 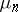 the sequences of their positive eigen values, listed in decreasing order, where each value is repeated as often as its multiplicity, then
the sequences of their positive eigen values, listed in decreasing order, where each value is repeated as often as its multiplicity, then 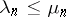 .
.
References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Wiley (1988) |
Minimax property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimax_property&oldid=19194