Lyapunov stochastic function
A non-negative function 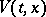 for which the pair
for which the pair 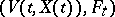 is a supermartingale for some random process
is a supermartingale for some random process 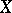 up to the instant
up to the instant 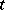 (cf. also Martingale). If
(cf. also Martingale). If 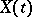 is a Markov process, then the Lyapunov stochastic function is a function for which the Lyapunov stochastic operator
is a Markov process, then the Lyapunov stochastic function is a function for which the Lyapunov stochastic operator
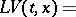 |
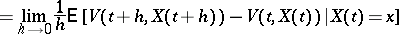 |
is non-positive. The operator 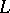 is the infinitesimal operator of the process
is the infinitesimal operator of the process 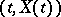 , and so the verification of the condition
, and so the verification of the condition 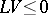 is easily carried out in specific cases. The operator
is easily carried out in specific cases. The operator  goes into the usual Lyapunov operator
goes into the usual Lyapunov operator  when the process
when the process 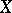 is determinate and is described by a system of differential equations. By means of the Lyapunov stochastic function it is possible to verify a number of qualitative properties of the trajectories of
is determinate and is described by a system of differential equations. By means of the Lyapunov stochastic function it is possible to verify a number of qualitative properties of the trajectories of 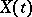 ; their role in the theory of random processes is similar to the role of the classical Lyapunov function in the theory of systems of differential equations.
; their role in the theory of random processes is similar to the role of the classical Lyapunov function in the theory of systems of differential equations.
Functions 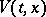 for which
for which 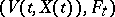 is not a supermartingale, but from which one can readily form a supermartingale, are sometimes also called Lyapunov stochastic functions. Below typical results are presented on the qualitative behaviour of trajectories of Markov processes in terms of a Lyapunov stochastic function.
is not a supermartingale, but from which one can readily form a supermartingale, are sometimes also called Lyapunov stochastic functions. Below typical results are presented on the qualitative behaviour of trajectories of Markov processes in terms of a Lyapunov stochastic function.
1) If 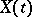 is a right-continuous strong Markov process in
is a right-continuous strong Markov process in 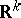 , defined up to the instant
, defined up to the instant  of first leaving an arbitrary compact set, and if there is a Lyapunov stochastic function
of first leaving an arbitrary compact set, and if there is a Lyapunov stochastic function 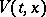 ,
, 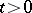 ,
, 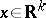 , and a constant
, and a constant  such that
such that
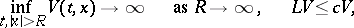 |
then
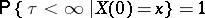 |
for any 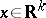 ; that is, the process
; that is, the process 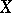 is defined for all
is defined for all 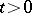 (is indefinitely extendable).
(is indefinitely extendable).
2) For the stationary Markov process in 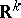 corresponding to a transition function
corresponding to a transition function 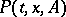 to exist it is sufficient that there should be a function
to exist it is sufficient that there should be a function 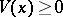 for which
for which
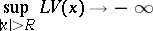 |
as 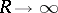 .
.
By means of the Lyapunov stochastic function one can carry over to Markov processes the main theorems of the direct Lyapunov method; these functions have also found application in the investigation of processes in discrete time.
References
| [1] | H.J. Kushner, "Stochastic stability and control" , Acad. Press (1967) |
| [2] | R.Z. [R.Z. Khas'minskii] Has'minskii, "Stochastic stability of differential equations" , Sijthoff & Noordhoff (1980) (Translated from Russian) |
| [3] | V.V. Kalashnikov, "Qualitative analysis of the behaviour of complex systems by the method of test functions" , Moscow (1978) (In Russian) |
Comments
The phrase stochastic Lyapunov function is more common than "Lyapunov stochastic function" .
Recently, stochastic Lyapunov functions have been used to prove convergence of recursive algorithms driven by stochastic processes. Convergence problems of this type arise in system identification and adaptive control.
References
| [a1] | G.C. Goodwin, P.J. Ramagadge, P.E. Caines, "Discrete time stochastic adaptive control" SIAM J. Control Optim. , 19 (1981) pp. 829–853 |
| [a2] | M. Metivier, P. Priouret, "Applications of a Kushner and Clark lemma to general classes of stochastic algorithms" IEEE Trans. Inform. Theory , 30 (1984) pp. 140–151 |
| [a3] | V. Solo, "The convergence of AML" IEEE Trans. Autom. Control , 24 (1979) pp. 958–962 |
| [a4] | J.H. van Schuppen, "Convergence results for continuous-time stochastic filtering algorithms" J. Math. Anal. Appl. , 96 (1983) pp. 209–225 |
Lyapunov stochastic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyapunov_stochastic_function&oldid=15796