Local topological group
A topological group in which the group operations are defined only for elements sufficiently close to the identity. The introduction of local topological groups was inspired by the study of the local structure of topological groups (that is, their structure in an arbitrary small neighbourhood of the identity, see [1]). The precise definition of a local topological group is as follows.
Let  be a topological space,
be a topological space,  an element of it,
an element of it, 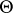 and
and  open subsets of
open subsets of  and
and 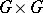 , respectively, where
, respectively, where 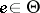 , and let
, and let  and
and 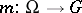 be continuous mappings. Then the system
be continuous mappings. Then the system 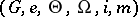 is called a local topological group if the following conditions are satisfied:
is called a local topological group if the following conditions are satisfied:
1) 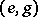 and
and  for any
for any 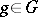 and
and 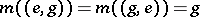 ;
;
2) if 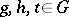 and
and 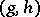 ,
,  ,
, 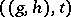 ,
,  , then
, then  ;
;
3) 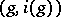 and
and 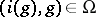 for any
for any 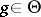 and
and 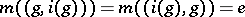 .
.
The local topological group  is usually denoted simply by
is usually denoted simply by  ; the element
; the element  is denoted by
is denoted by 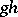 and called the product of
and called the product of 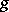 and
and 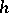 ; the element
; the element 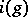 is denoted by
is denoted by 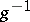 and called the inverse of
and called the inverse of 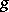 ; the element
; the element  is called the identity of
is called the identity of  . If
. If 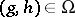 , one says that the product of
, one says that the product of 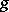 and
and 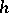 is defined; if
is defined; if 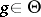 , one says that an inverse element is defined for
, one says that an inverse element is defined for 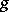 .
.
These operations on 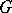 (which are not defined for all elements) induce the structure of a local topological group in an arbitrary neighbourhood of the identity
(which are not defined for all elements) induce the structure of a local topological group in an arbitrary neighbourhood of the identity  of
of 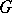 . Let
. Let 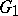 and
and 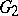 be two local topological groups. A local homomorphism of
be two local topological groups. A local homomorphism of 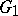 into
into 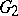 is a continuous mapping
is a continuous mapping  of a neighbourhood
of a neighbourhood 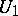 of the identity
of the identity 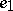 of
of 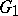 into a neighbourhood
into a neighbourhood 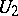 of the identity
of the identity 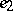 of
of 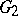 such that
such that 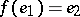 and for any elements
and for any elements  whose product is defined in
whose product is defined in 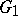 the product of the elements
the product of the elements  and
and  is also defined in
is also defined in 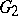 and
and  . Two local homomorphisms of
. Two local homomorphisms of 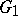 into
into 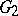 are said to be equivalent if they coincide in a neighbourhood of the identity of
are said to be equivalent if they coincide in a neighbourhood of the identity of 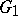 . Suppose that the local homomorphism
. Suppose that the local homomorphism 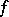 is a homeomorphism of the neighbourhoods
is a homeomorphism of the neighbourhoods 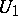 and
and 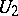 and that the inverse mapping
and that the inverse mapping 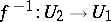 is a local homomorphism of
is a local homomorphism of 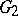 to
to 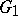 . Then
. Then  is called a local isomorphism of
is called a local isomorphism of 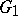 and
and 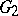 . Two local topological groups between which there is a local isomorphism are said to be locally isomorphic. For example, any local topological group is locally isomorphic to an arbitrary neighbourhood of the identity of it.
. Two local topological groups between which there is a local isomorphism are said to be locally isomorphic. For example, any local topological group is locally isomorphic to an arbitrary neighbourhood of the identity of it.
As an example of a local topological group one can take any topological group (and hence any neighbourhood of the identity of it). In the theory of local topological groups the main question is to what extent this example has a general character; that is, whether any local topological group is locally isomorphic to some topological group. In the general case the answer is negative (see [4]), but in the important special case of finite-dimensional local Lie groups (cf. Lie group, local) it is affirmative.
Just as in the theory of topological groups, in the theory of local topological groups one can define the concepts of (local) subgroups, normal subgroups, cosets, and quotient groups. For example, let  be a local topological group and let
be a local topological group and let 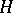 be a subset of
be a subset of 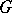 containing
containing  such that in a neighbourhood
such that in a neighbourhood 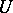 of
of  in
in  the set
the set 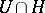 is closed. Suppose also that for any
is closed. Suppose also that for any 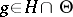 the element
the element 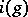 belongs to
belongs to 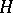 and that the set
and that the set
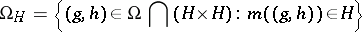 |
is open in 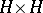 (under the assumption that
(under the assumption that  is endowed with the topology induced from
is endowed with the topology induced from 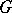 ). Then the system
). Then the system
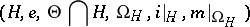 |
is a local topological group, called a local subgroup of 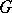 . For the definitions of a normal subgroup, cosets with respect to a subgroup and a quotient group, see [1].
. For the definitions of a normal subgroup, cosets with respect to a subgroup and a quotient group, see [1].
References
| [1] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [2] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [4] | S. Lie, F. Engel, "Theorie der Transformationsgruppen" , 1–3 , Leipzig (1930) |
Local topological group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_topological_group&oldid=17379