The radius of the circle along which an electrically charged particle moves in a plane perpendicular to a magnetic field with magnetic induction  . The motion of the charge
. The motion of the charge  in a uniform magnetic field takes place under the action of the Lorentz force and is described by the equation
in a uniform magnetic field takes place under the action of the Lorentz force and is described by the equation
 | (1) |
where  is the momentum of the charged particle and
is the momentum of the charged particle and  is the velocity of the charge in the laboratory reference frame. The solution of (1) in a Cartesian coordinate system with the
is the velocity of the charge in the laboratory reference frame. The solution of (1) in a Cartesian coordinate system with the  -axis directed along the field
-axis directed along the field  has the form
has the form
 | (2) |
where 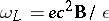 is the so-called Larmor frequency,
is the so-called Larmor frequency,  is the energy of the charged particle, which does not change under motion in a uniform magnetic field,
is the energy of the charged particle, which does not change under motion in a uniform magnetic field,  ,
, 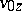 ,
, 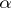 ,
, 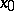 ,
,  ,
, 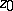 are constants determined from the initial conditions, and
are constants determined from the initial conditions, and
is the Larmor radius. In a uniform magnetic field the charge moves along a helix with axis along the magnetic field and Larmor radius  . The velocity of the particle is constant.
. The velocity of the particle is constant.
If the velocity of the particle is small compared with the velocity of light, one can put approximately  and the expression for the Larmor radius takes the form
and the expression for the Larmor radius takes the form
The magnetic moment of the system manifests itself as a result of the rotation of the charged particles in the magnetic field.
References
| [1] | I.E. Tamm, "Fundamentals of the theory of electricity" , MIR (1979) (Translated from Russian) |
| [2] | L.D. Landau, E.M. Lifshitz, "The classical theory of fields" , Addison-Wesley (1951) (Translated from Russian) |
References
| [a1] | P.C. Clemmow, J.P. Dougherty, "Electrodynamics of particles and plasmas" , Addison-Wesley (1969) |
How to Cite This Entry:
Larmor radius. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Larmor_radius&oldid=15742
This article was adapted from an original article by V.V. Parail (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article . The motion of the charge
. The motion of the charge  in a uniform magnetic field takes place under the action of the Lorentz force and is described by the equation
in a uniform magnetic field takes place under the action of the Lorentz force and is described by the equation

 is the momentum of the charged particle and
is the momentum of the charged particle and  is the velocity of the charge in the laboratory reference frame. The solution of (1) in a Cartesian coordinate system with the
is the velocity of the charge in the laboratory reference frame. The solution of (1) in a Cartesian coordinate system with the  -axis directed along the field
-axis directed along the field  has the form
has the form

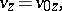


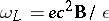 is the so-called Larmor frequency,
is the so-called Larmor frequency,  is the energy of the charged particle, which does not change under motion in a uniform magnetic field,
is the energy of the charged particle, which does not change under motion in a uniform magnetic field,  ,
, 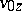 ,
, 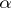 ,
, 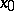 ,
,  ,
, 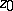 are constants determined from the initial conditions, and
are constants determined from the initial conditions, and
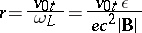
 . The velocity of the particle is constant.
. The velocity of the particle is constant.
 and the expression for the Larmor radius takes the form
and the expression for the Larmor radius takes the form
