Landau theorems

Theorems for functions regular in a disc, which establish some connections between geometrical properties of the conformal mapping that is induced by these functions and the initial coefficients of the power series that represent them.

In 1904 E. Landau showed [1] that if a function 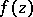is regular in the disc and does not take the values 0 and 1 in it, then is bounded from above by a positive constant that depends only on 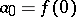and . In 1905 C. Carathéodory established that the role of extremal function in this theorem is played by a modular function. These results of Landau and Carathéodory are known in the form of the following theorem.

The Landau–Carathéodory theorem. If the function

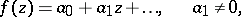is regular and does not take the values 0 and 1 in the disc 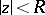, then

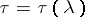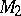here is a branch of the function inverse to the classical modular function of the group of fractional-linear transformations

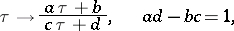where and 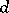are odd numbers an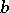d and are even numbers. The function 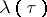maps the fundamental domain 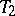of :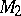

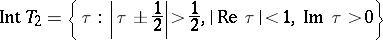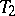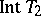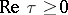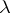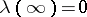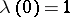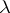( is obtained by adjoining to that part of the boundary for which ) onto the whole extended -plane in such a way that , , . For each value of the equation 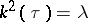has one and only one solution belonging to 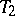. The function 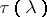in the Landau–Carathéodory theorem can be understood as the branch of the inverse function that maps the extended -plane onto .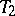

The example of the function 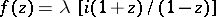, regular in the disc 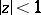and not equal to 0 or 1 for 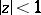, shows that the Landau–Carathéodory theorem cannot be improved. The Landau–Carathéodory theorem implies the Picard theorem on values that cannot be taken by entire functions.

Landau found the exact value of the constant that occurs in the following formulation of the Cauchy theorem on inverse functions. Suppose that the function 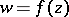is regular in the disc 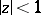and that , and 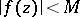in the disc 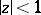, where 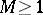; then there is a constant 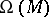such that the inverse function , which vanishes at , is regular in the disc and in this disc. Landau established that

The extremal function attaining this bound is

This function 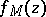is extremal in the following theorem of Landau. If a function 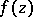satisfies the conditions mentioned above, then 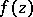is single-valued in the disc , where .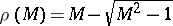

Landau has also established a number of covering theorems in the theory of conformal mapping that establish the existence of and bounds for the corresponding constants. One of them is given below. Let 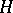be the class of functions 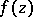regular in 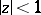and normalized by the conditions , . Bloch's theorem (see Bloch constant) implies the following theorem of Landau: There is an absolute constant

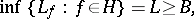where 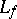is the radius of the largest disc in the 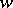-plane that is entirely covered by the image of the disc 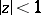under the mapping 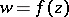, and 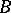is Bloch's constant. The constant 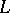is called Landau's constant. The following bounds for 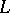are known (see [5], [8]): 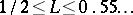. The Picard theorem again follows from this theorem.

References

[1]	E. Landau, "Ueber eine Verallgemeinerung des Picardschen Satzes" Sitzungsber. Preuss. Akad. Wiss. , 38 (1904) pp. 1118–1133
[2]	E. Landau, D. Gaier, "Darstellung und Begründung einiger neuerer Ergebnisse der Funktionentheorie" , Springer, reprint (1986)
[3]	E. Landau, "Zum Koebeschen Verzerrungssatz" Rend. Circ. Mat. Palermo , 46 (1922) pp. 347–348
[4]	E. Landau, "Der Picard–Schottkysche Satz und die Blochsche Konstante" Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl. , 32 (1926) pp. 467–474
[5]	E. Landau, "Ueber die Blochsche Konstante und zwei verwandte Weltkonstanten" Math. Z. , 30 (1929) pp. 608–634
[6]	E. Landau, "Ansgewählte Kapitel der Funktionentheorie" Trudy Tbilis. Mat. Inst. Akad. Nauk. SSSR , 8 (1940) pp. 23–68
[7]	S. Stoilov, "The theory of functions of a complex variable" , 1–2 , Moscow (1962) (In Russian; translated from Rumanian)
[8]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[9]	G. Valiron, "Les fonctions analytiques" , Paris (1954)
[10]	A. Bermant, "Dilatation of a modular function and reconstruction problems" Mat. Sb. , 15 : 2 (1944) pp. 285–318 (In Russian) (French abstract)

Comments

It is now (1989) known that the Landau constant 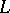satisfies

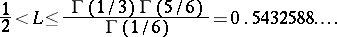The upper bound is over half a century old and is due to R. Robinson and, independently, H. Rademacher [a1]. See [a2] for more detailed information on these and related questions.

References

[a1]	H. Rademacher, "On the Bloch–Landau constant" Amer. J. Math. , 65 (1943) pp. 387–390
[a2]	C.D. Minda, "Bloch constants" J. d'Anal. Math. , 41 (1982) pp. 54–84