Julia theorem
If  is an isolated essential singular point of an analytic function
is an isolated essential singular point of an analytic function 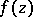 of the complex variable
of the complex variable  , then there exists at least one ray
, then there exists at least one ray 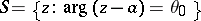 issuing from
issuing from  such that in every angle
such that in every angle
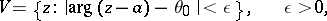 |
that is symmetric with respect to the ray, 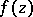 assumes every finite value, except possibly one, at an infinite sequence of points
assumes every finite value, except possibly one, at an infinite sequence of points 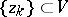 converging to
converging to  . This result of G. Julia (see [1]) supplements the big Picard theorem on the behaviour of an analytic function in a neighbourhood of an essential singularity.
. This result of G. Julia (see [1]) supplements the big Picard theorem on the behaviour of an analytic function in a neighbourhood of an essential singularity.
The rays figuring in Julia's theorem are called Julia rays. Thus, for 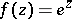 and
and 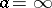 , the Julia rays are the positive and negative parts of the imaginary axis. In connection with Julia's theorem, a Julia segment or a Julia chord for a function
, the Julia rays are the positive and negative parts of the imaginary axis. In connection with Julia's theorem, a Julia segment or a Julia chord for a function 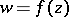 meromorphic in, for example, the unit disc
meromorphic in, for example, the unit disc 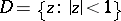 , is a chord
, is a chord  with end point
with end point 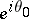 on the circumference
on the circumference  such that in every open angle
such that in every open angle 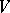 with vertex
with vertex 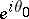 and containing
and containing 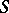 the function
the function  assumes all values on the Riemann
assumes all values on the Riemann 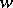 -sphere, except possibly two. The point
-sphere, except possibly two. The point 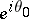 is called a Julia point for
is called a Julia point for 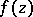 if every chord
if every chord  with end point
with end point 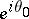 is a Julia chord for
is a Julia chord for 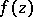 . There exist meromorphic functions of bounded characteristic for which every point on
. There exist meromorphic functions of bounded characteristic for which every point on  is a Julia point.
is a Julia point.
See also Asymptotic value; Iversen theorem; Cluster set.
References
| [1] | G. Julia, "Leçons sur les fonctions uniformes à une point singulier essentiel isolé" , Gauthier-Villars (1924) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. 345 (Translated from Russian) |
Comments
Instead of Julia ray the term Julia direction is also used.
Julia theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Julia_theorem&oldid=11784