Infinitely-divisible distributions, factorization of
A representation of infinitely-divisible distributions in the form of the convolution of certain probability distributions. The distributions which participate in the factorization of infinitely-divisible distributions are called the components in the factorization.
Certain factorizations of infinitely-divisible distributions may have components which are not infinitely divisible [1]. An important task in the theory of factorization of infinitely-divisible distributions is the description of the class 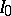 of infinitely-divisible distributions with exclusively infinitely-divisible components. The representatives of
of infinitely-divisible distributions with exclusively infinitely-divisible components. The representatives of 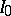 include the normal distribution, the Poisson distribution and their compositions (cf. Lévy–Cramér theorem).
include the normal distribution, the Poisson distribution and their compositions (cf. Lévy–Cramér theorem).
An important role in the description of the class 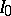 is played by Linnik's class
is played by Linnik's class 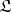 of infinitely-divisible distributions [2], in which the function
of infinitely-divisible distributions [2], in which the function 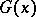 in the Lévy–Khinchin canonical representation is a step function with jumps at the points between
in the Lévy–Khinchin canonical representation is a step function with jumps at the points between 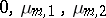 ,
, 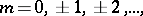 where
where  ,
, 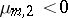 , and the numbers
, and the numbers 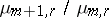 (
(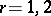 ;
; 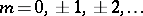 ) are natural numbers other than 1. If the infinitely-divisible distribution is such that
) are natural numbers other than 1. If the infinitely-divisible distribution is such that 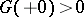 , it can only belong to
, it can only belong to 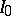 if it belongs to
if it belongs to 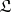 . This condition is not sufficient, but it is known that a distribution of
. This condition is not sufficient, but it is known that a distribution of 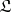 belongs to
belongs to 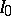 if
if
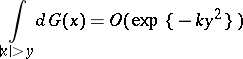 |
for some 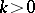 and
and 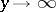 .
.
If 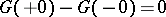 , belonging to
, belonging to 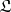 is not a necessary condition for belonging to
is not a necessary condition for belonging to 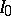 . For instance, all infinitely-divisible distributions in which the function
. For instance, all infinitely-divisible distributions in which the function 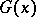 is constant for
is constant for 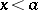 and
and  , where
, where 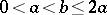 , belong to
, belong to  .
.
The following is a simple sufficient condition for an infinitely-divisible distribution not to belong to 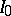 . The inequality
. The inequality 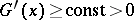 must be fulfilled on the interval
must be fulfilled on the interval  , where
, where 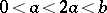 . It follows from this condition that a stable distribution, except the normal distribution and the unit distribution, as well as the gamma-distribution and the
. It follows from this condition that a stable distribution, except the normal distribution and the unit distribution, as well as the gamma-distribution and the  -distribution, does not belong to
-distribution, does not belong to 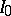 .
.
The class 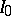 is dense in the class of all infinitely-divisible distributions in the topology of weak convergence; all infinitely-divisible distributions can be represented as compositions of a finite or countable set of distributions from
is dense in the class of all infinitely-divisible distributions in the topology of weak convergence; all infinitely-divisible distributions can be represented as compositions of a finite or countable set of distributions from 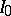 .
.
References
| [1] | A.Ya. Khinchin, "Contribution à l'arithmétique des lois de distribution" Byull. Moskov. Gos. Univ. (A) , 1 : 1 (1937) pp. 6–17 |
| [2] | Yu.V. Linnik, "General theorems on factorization of infinitely divisible laws" Theory Probab. Appl. , 3 : 1 (1958) pp. 1–37 Teor. Veroyatnost. i Primenen. , 3 : 1 (1958) pp. 3–40 |
| [3] | Yu.V. Linnik, "Decomposition of probability laws" , Oliver & Boyd (1964) (Translated from Russian) |
| [4] | Yu.V. Linnik, I.V. Ostrovskii, "Decomposition of random variables and vectors" , Amer. Math. Soc. (1977) (Translated from Russian) |
| [5] | B. Ramachandran, "Advanced theory of characteristic functions" , Statist. Publ. Soc. , Calcutta (1967) |
| [6] | E. Lukacs, "Characteristic functions" , Griffin (1970) |
| [7] | L.Z. Livshits, I.V. Ostrovskii, G.P. Chistyakov, "Arithmetic of probability laws" J. Soviet Math. , 6 : 2 (1976) pp. 99–122 Itogi Nauk. i Tekhn. Teor. Veroyatnost. Mat. Statist. Teoret. Kibernetika , 12 (1975) pp. 5–42 |
| [8] | I.V. Ostrovskii, "The arithmetic of probability distributions" Theor. Probab. Appl. , 31 : 1 (1987) pp. 1–24 Teor. Veroyatnost. i Primenen. , 31 : 1 (1986) pp. 3–30 |
Comments
References
| [a1] | E. Lukacs, "Developments in characteristic function theory" , Griffin (1983) |
Infinitely-divisible distributions, factorization of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Infinitely-divisible_distributions,_factorization_of&oldid=12413