Homological dimension of a space

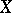with respect to a coefficient group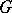

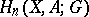The largest integer for which the Aleksandrov–Čech homology group of some closed set 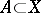is non-zero. The homological dimension is denoted by 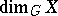. The cohomological dimension — the least integer for which the mapping 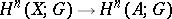is epimorphic for all closed 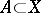— is defined in an analogous manner. Homological dimension theory is usually understood to mean its cohomological variant, which has been much more thoroughly studied. This is because Aleksandrov–Čech cohomology satisfies all the Steenrod–Eilenberg axioms, including exactness, so that the use of cohomology proved to be more effective. In the category of metrizable compacta, where the groups 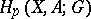and 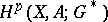are connected by Pontryagin duality, the homological approach with coefficients in a compact group 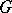is equivalent to the cohomological approach with coefficients in the dual group 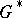. Similarly, both approaches are equivalent if the elements of the same field 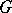are taken as coefficients.

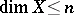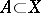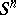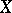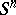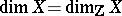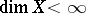Homological dimension theory originated from a theorem by P.S. Aleksandrov: The relation , where dim is the Lebesgue dimension, is equivalent to saying that any continuous mapping from an arbitrary closed set into the -dimensional sphere can be extended to a mapping from all of into . It follows that if and 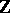is the group of integers. It was subsequently noted by L.S. Pontryagin that homological dimensions with respect to different coefficient groups need not coincide (the general result which follows from the universal coefficient formula is that 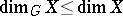for any compactum 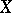). Homological dimension, like Lebesgue dimension, is a topological invariant of the space .

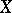The homological dimension 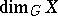has many of the properties of the ordinary dimension dim. In fact, if 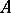is a closed subset of 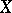, then 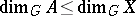; if 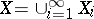, where each 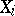is closed in 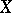, then

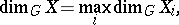etc. Aleksandrov's obstruction theorem is valid: Subsets of the Euclidean space 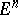of homological dimension are (locally) knotted by 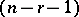-dimensional cycles. See also Dimension.

An important point in homological dimension theory is the relation between homological dimensions with respect to different coefficient groups. The problems arising in this context have many immediate applications to dimension theory, and are closely connected with some of the most important problems in the theory of transformation groups. The analysis of dimensions of products is very important. Thus,

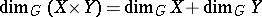if 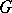is the field of rational numbers or the field of residues modulo a prime number, and

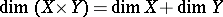for any compactum 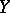(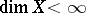) if and only if all dimensions 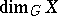coincide with .

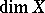The essential features of homological dimension theory have undergone substantial changes with the introduction of sheaf theory as a research tool; cohomological dimension theory with coefficients in a sheaf has undergone an independent development (the fundamental definition is the same). The new methods proved to be applicable in solving many problems related to the behaviour of dimensions under continuous mappings, and also made it possible to extend the domain of application of the theory to the category of paracompact spaces (cf. Paracompact space).

References

[1]	H. Wallman, "Dimension theory" , Princeton Univ. Press (1948)
[2]	V.I. Kuz'minov, "Homological dimension theory" Russian Math. Surveys , 23 : 5 (1968) pp. 1–45 Uspekhi Mat. Nauk , 23 : 5 (1968) pp. 3–49

Comments

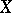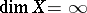Recently A.N. Dranishnikov constructed a compact space with and 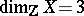. Thus, the condition 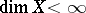is necessary for the equality .

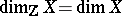References

[a1]	A.N. Dranishnikov, "On a problem of P.S. Aleksandrov" Mat. Sb. , 135 (1988) pp. 551–557 (In Russian)
[a2]	J.-I. Nagata, "Modern dimension theory" , Noordhoff (1965)