Homological containment
A method for characterizing the dimension of a compactum lying in a Euclidean space 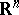 in terms of metric properties of the complementary space. The essential measure of a cycle
in terms of metric properties of the complementary space. The essential measure of a cycle  in a compactum
in a compactum 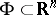 is taken to be the least upper bound of those
is taken to be the least upper bound of those 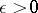 for which it is possible to select a compact support
for which it is possible to select a compact support  of the cycle
of the cycle  such that the cycle is not homologous to zero in
such that the cycle is not homologous to zero in 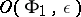 . The
. The 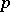 -dimensional homological diameter
-dimensional homological diameter 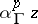 of a cycle
of a cycle  in an open set
in an open set 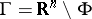 is the greatest lower bound of the
is the greatest lower bound of the 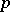 -dimensional diameters of the bodies of all cycles that are homologous in
-dimensional diameters of the bodies of all cycles that are homologous in 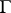 to
to  . Here, the
. Here, the 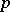 -dimensional diameter
-dimensional diameter 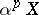 of a compactum
of a compactum 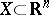 is the greatest lower bound of those
is the greatest lower bound of those 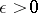 for which there exists a continuous
for which there exists a continuous  -shift of
-shift of  in a
in a 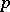 -dimensional compactum (and thus in a polyhedron).
-dimensional compactum (and thus in a polyhedron).
Any 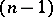 -dimensional cycle of the open set
-dimensional cycle of the open set 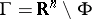 which is linked with each point of the compactum
which is linked with each point of the compactum 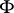 is said to be a pocket around
is said to be a pocket around 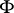 .
.
The pocket theorem. Let  . Then there exists an
. Then there exists an 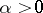 such that any pocket around
such that any pocket around  has
has 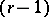 -dimensional homological diameter larger than
-dimensional homological diameter larger than 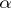 , while the
, while the  -dimensional homological diameter of any cycle in
-dimensional homological diameter of any cycle in 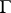 is zero. Pockets around
is zero. Pockets around 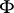 with arbitrary small essential measure always exist in this situation. On the other hand, if
with arbitrary small essential measure always exist in this situation. On the other hand, if 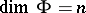 , then there exists an
, then there exists an 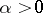 such that for any pocket
such that for any pocket 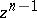 around
around 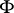 the inequality
the inequality 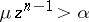 is true (here,
is true (here, 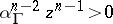 and
and 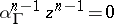 for any pocket
for any pocket 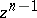 ).
).
The pocket theorem may be further strengthened using the concept of a zone around a compactum.
The zone theorem. Let 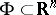 be a compactum of dimension
be a compactum of dimension  . There exists a
. There exists a 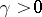 such that for any
such that for any 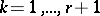 and any
and any 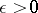 there exists in
there exists in  an
an 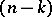 -dimensional cycle
-dimensional cycle  (a zone of dimension
(a zone of dimension  around
around 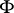 ), for
), for  bounding in
bounding in 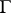 , for which
, for which 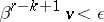 ,
, 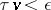 . Furthermore, for any cycle
. Furthermore, for any cycle 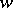 homologous to
homologous to  in the
in the 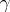 -neighbourhood of the latter with respect to
-neighbourhood of the latter with respect to 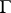 the inequality
the inequality 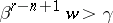 is valid; for any chain
is valid; for any chain  bounded by the cycle
bounded by the cycle  in
in 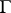 one has
one has 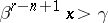 .
.
On the other hand, if 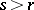 and if
and if 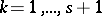 , then, for any
, then, for any 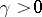 , any
, any 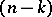 -dimensional cycle
-dimensional cycle  in
in 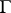 for which
for which 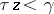 is homologous in its
is homologous in its 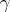 -neighbourhood (with respect to
-neighbourhood (with respect to 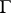 ) to some cycle
) to some cycle 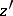 with
with 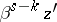 arbitrary small. Furthermore, if
arbitrary small. Furthermore, if 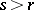 and if
and if 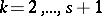 , then for any
, then for any 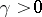 any
any  -dimensional cycle
-dimensional cycle  , bounding in
, bounding in 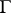 , for which
, for which 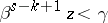 (and
(and 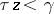 if
if  ) bounds in
) bounds in  a chain
a chain  with
with 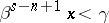 . Here
. Here 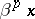 ,
, 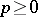 , is the greatest lower bound of those
, is the greatest lower bound of those 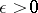 for which there exists an
for which there exists an  -shift of the vertices of the chain
-shift of the vertices of the chain  by means of which
by means of which  becomes degenerate up to dimension
becomes degenerate up to dimension 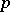 ;
; 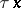 is the greatest lower bound of those
is the greatest lower bound of those 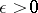 for which there exists an
for which there exists an  -shift of the vertices of
-shift of the vertices of  converting
converting  to a zero chain.
to a zero chain.
References
| [1] | P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian) |
Comments
An  -shift of a subspace
-shift of a subspace 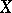 contained in some Euclidean space
contained in some Euclidean space  is a mapping
is a mapping  such that the distance of
such that the distance of  to
to 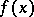 is less than
is less than  for all
for all  .
.
Homological containment. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homological_containment&oldid=14317