Homoclinic bifurcations
Consider an autonomous system of ordinary differential equations depending on a parameter
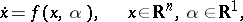 | (a1) |
where 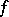 is smooth. Denote by
is smooth. Denote by 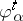 the flow (continuous-time dynamical system) corresponding to (a1). Let
the flow (continuous-time dynamical system) corresponding to (a1). Let 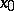 be an equilibrium of the system at
be an equilibrium of the system at 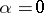 . An orbit
. An orbit 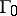 starting at a point
starting at a point  is called homoclinic to the equilibrium point
is called homoclinic to the equilibrium point 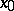 of (a1) at
of (a1) at 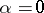 if
if 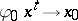 as
as 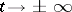 . Generically, presence of a homoclinic orbit at
. Generically, presence of a homoclinic orbit at 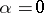 implies a global codimension-one bifurcation of (a1), since the homoclinic orbit disappears for all sufficiently small
implies a global codimension-one bifurcation of (a1), since the homoclinic orbit disappears for all sufficiently small 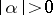 . Moreover, the disappearance of a homoclinic orbit leads to the creation or destruction of one (or more) limit cycle nearby. When such a cycle approaches the homoclinic orbit
. Moreover, the disappearance of a homoclinic orbit leads to the creation or destruction of one (or more) limit cycle nearby. When such a cycle approaches the homoclinic orbit 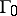 as
as 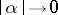 , its period tends to infinity. In some cases, there are infinitely many limit cycles in a neighbourhood of
, its period tends to infinity. In some cases, there are infinitely many limit cycles in a neighbourhood of  for sufficiently small
for sufficiently small 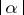 , since the Poincaré return map near the homoclinic orbit demonstrates Smale's horseshoes [a14] and their associated shift dynamics.
, since the Poincaré return map near the homoclinic orbit demonstrates Smale's horseshoes [a14] and their associated shift dynamics.
First, consider the case when 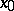 is an hyperbolic equilibrium, i.e. the Jacobian matrix
is an hyperbolic equilibrium, i.e. the Jacobian matrix 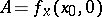 has no eigenvalues on the imaginary axis. Suppose that
has no eigenvalues on the imaginary axis. Suppose that 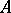 has
has 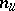 eigenvalues with positive real part
eigenvalues with positive real part
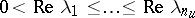 |
and 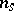 eigenvalues with negative real part
eigenvalues with negative real part
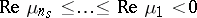 |
(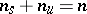 ). The equilibrium
). The equilibrium 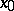 has unstable and stable invariant manifolds
has unstable and stable invariant manifolds 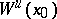 and
and 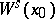 composed by outgoing and incoming orbits, respectively;
composed by outgoing and incoming orbits, respectively; 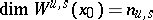 .
.
The eigenvalues with positive (negative) real part that are closest to the imaginary axis are called the unstable (stable) leading eigenvalues, while the corresponding eigenspaces are called the unstable (stable) leading eigenspaces. Almost all orbits on the stable and unstable manifolds tend to the equilibrium 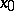 as
as 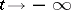 (
(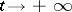 ) along the corresponding leading eigenspace. Exceptional orbits form a non-leading manifold tangent to the eigenspace corresponding to the non-leading eigenvalues.
) along the corresponding leading eigenspace. Exceptional orbits form a non-leading manifold tangent to the eigenspace corresponding to the non-leading eigenvalues.
The saddle quantity 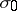 of a hyperbolic equilibrium is the sum of the real parts of its leading eigenvalues:
of a hyperbolic equilibrium is the sum of the real parts of its leading eigenvalues: 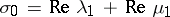 , where
, where 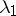 is a leading unstable eigenvalue and
is a leading unstable eigenvalue and 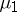 is a leading stable eigenvalue. Generically, leading eigenspaces are either one- or two-dimensional. In the first case, an eigenspace corresponds to a simple real eigenvalue, while in the second case it corresponds to a simple pair of complex-conjugate eigenvalues. Reversing the time direction, if necessary, one has only three typical configurations of the leading eigenvalues:
is a leading stable eigenvalue. Generically, leading eigenspaces are either one- or two-dimensional. In the first case, an eigenspace corresponds to a simple real eigenvalue, while in the second case it corresponds to a simple pair of complex-conjugate eigenvalues. Reversing the time direction, if necessary, one has only three typical configurations of the leading eigenvalues:
a) (saddle) the leading eigenvalues are real and simple: 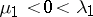 ;
;
b) (saddle-focus) the stable leading eigenvalues are non-real and simple: 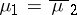 ,
, 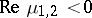 , while the unstable leading eigenvalue
, while the unstable leading eigenvalue 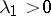 is real and simple;
is real and simple;
c) (focus-focus) the leading eigenvalues are non-real and simple:
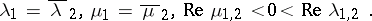 |
The following theorems by A.A. Andronov and E.A. Leontovich [a1] (in the saddle case when 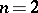 ) and L.P. Shil'nikov (otherwise) [a11], [a13] are valid (see also [a15], [a2], [a5]).
) and L.P. Shil'nikov (otherwise) [a11], [a13] are valid (see also [a15], [a2], [a5]).
(Saddle) For any generic one-parameter system (a1) having a saddle equilibrium point 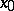 with a homoclinic orbit
with a homoclinic orbit 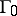 at
at  , there exists a neighbourhood
, there exists a neighbourhood 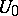 of
of 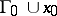 in which a unique limit cycle
in which a unique limit cycle 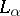 bifurcates from
bifurcates from 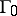 as
as 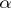 passes through zero. Moreover,
passes through zero. Moreover, 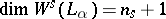 if
if 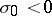 , and
, and 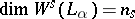 if
if  .
.
(Saddle-focus) For any generic one-parameter system (a1) having a saddle-focus equilibrium point  with a homoclinic orbit
with a homoclinic orbit 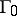 at
at 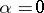 , there exists a neighbourhood
, there exists a neighbourhood 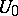 of
of 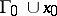 such that one of the following alternatives holds:
such that one of the following alternatives holds:
a) if 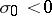 , a unique limit cycle
, a unique limit cycle 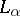 bifurcates from
bifurcates from 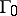 in
in 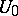 as
as 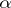 passes through zero,
passes through zero, 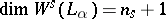 ;
;
b) if 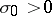 , the system has an infinite number of saddle limit cycles in
, the system has an infinite number of saddle limit cycles in 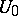 for all sufficiently small
for all sufficiently small 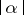 .
.
(Focus-focus) For any generic one-parameter system (a1) having a focus-focus equilibrium point 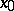 with a homoclinic orbit
with a homoclinic orbit 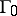 at
at 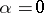 , there exists a neighbourhood
, there exists a neighbourhood 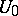 of
of 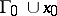 in which the system has an infinite number of saddle limit cycles in
in which the system has an infinite number of saddle limit cycles in 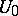 for all sufficiently small
for all sufficiently small 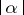 .
.
The genericity conditions mentioned above have some common parts:
1) the leading eigenspaces are either one- or two-dimensional and 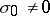 ;
;
2) 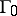 tends to
tends to 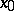 as
as 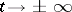 along the leading eigenspaces;
along the leading eigenspaces;
3) the intersection of the tangent spaces to 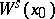 and
and 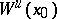 at each point on
at each point on  is one-dimensional;
is one-dimensional;
4) 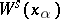 and
and 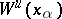 split by an
split by an 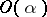 distance as
distance as 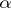 moves away from zero, where
moves away from zero, where 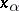 is the continuation of
is the continuation of 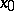 for small
for small 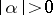 .
.
There is also a case-dependent non-degeneracy condition dealing with the global topology of 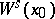 and
and 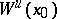 around
around 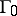 at
at 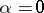 . The exact formulation of this condition can be found in [a2]. In the planar case (
. The exact formulation of this condition can be found in [a2]. In the planar case (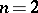 ), only conditions 1) and 4) are relevant.
), only conditions 1) and 4) are relevant.
Suppose now that 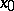 is a non-hyperbolic equilibrium of (a1) at
is a non-hyperbolic equilibrium of (a1) at 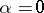 , having a homoclinic orbit
, having a homoclinic orbit 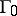 . Only the case when
. Only the case when 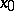 has a simple zero eigenvalue and no other eigenvalues on the imaginary axis (i.e.,
has a simple zero eigenvalue and no other eigenvalues on the imaginary axis (i.e., 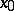 is a saddle-node, cf. Saddle node) appears in generic one-parameter families (has codimension-one). If the saddle-node has a single homoclinic orbit
is a saddle-node, cf. Saddle node) appears in generic one-parameter families (has codimension-one). If the saddle-node has a single homoclinic orbit 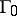 , then, generically, a unique limit cycle bifurcates from
, then, generically, a unique limit cycle bifurcates from 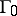 , when the saddle-node disappears via the fold bifurcation. The cycle can be either attracting/repelling or saddle type, depending on the location of the non-zero eigenvalues of
, when the saddle-node disappears via the fold bifurcation. The cycle can be either attracting/repelling or saddle type, depending on the location of the non-zero eigenvalues of 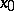 on the complex plane. If the saddle-node has more than two homoclinic orbits,
on the complex plane. If the saddle-node has more than two homoclinic orbits, 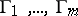 , then, generically, infinitely many saddle limit cycles appear from
, then, generically, infinitely many saddle limit cycles appear from 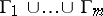 , when the equilibrium
, when the equilibrium 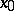 disappears. The genericity conditions include the non-degeneracy of the underlying fold bifurcation, as well as the requirement that
disappears. The genericity conditions include the non-degeneracy of the underlying fold bifurcation, as well as the requirement that  departs and returns to the saddle-node along the null-vector of the Jacobian matrix evaluated at
departs and returns to the saddle-node along the null-vector of the Jacobian matrix evaluated at  for
for 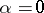 . The two-dimensional case has been treated in [a1]. The cases with
. The two-dimensional case has been treated in [a1]. The cases with 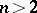 were considered by Shil'nikov [a9], [a12] and presented in [a2], [a5].
were considered by Shil'nikov [a9], [a12] and presented in [a2], [a5].
In generic discrete-time dynamical systems defined by iterations of diffeomorphisms, orbits which are homoclinic to a hyperbolic fixed point persist under small parameter variations. Stable and unstable manifolds of the fixed point intersect transversally along the homoclinic orbits, implying the existence of the Poincaré homoclinic structure with infinitely many saddle periodic orbits [a14], [a7], [a10], [a8], [a6]. The homoclinic structure appears/disappears via a non-transversal homoclinic bifurcation, when the stable and the unstable manifolds of the fixed point become tangent along the homoclinic orbit [a3], [a4], [a16].
References
| [a1] | A.A. Andronov, E.A. Leontovich, I.I. Gordon, A.G. Maier, "Theory of bifurcations of dynamical systems on a plane" , Israel Program Sci. Transl. (1971) (In Russian) |
| [a2] | V.I. Arnol'd, V.S. Afraimovich, Yu.S. Il'yashenko, L.P. Shil'nikov, "Bifurcation theory" V.I. Arnol'd (ed.) , Dynamical Systems V , Encycl. Math. Sci. , Springer (1994) (In Russian) |
| [a3] | N.K. Gavrilov, L.P. Shilnikov, "On three-dimensional systems close to systems with a structurally unstable homoclinic curve: I" Mat. USSR Sb. , 17 (1972) pp. 467–485 (In Russian) |
| [a4] | N.K. Gavrilov, L.P. Shilnikov, "On three-dimensional systems close to systems with a structurally unstable homoclinic curve: II" Mat. USSR Sb. , 19 (1973) pp. 139–156 (In Russian) |
| [a5] | Yu.A. Kuznetsov, "Elements of applied bifurcation theory" , Springer (1995) |
| [a6] | J. Moser, "Stable and random motions in dynamical systems" , Princeton Univ. Press (1973) |
| [a7] | Yu.I. Neimark, "On motions close to a bi-asymptotic motion" Dokl. AKad. Nauk SSSR , 142 (1967) pp. 1021–1024 (In Russian) |
| [a8] | Z. Nitecki, "Differentiable dynamics" , MIT (1971) |
| [a9] | L.P. Shil'nikov, "On the generation of a periodic motion from a trajectory which leaves and re-enters a saddle-saddle state of equilibrium" Soviet Math. Dokl. , 7 (1966) pp. 1155–1158 (In Russian) |
| [a10] | L.P. Shil'nikov, "On a Poincaré–Birkhoff problem" Mat. USSR Sb. , 3 (1967) pp. 353–371 (In Russian) |
| [a11] | L.P. Shil'nikov, "On the generation of periodic motion from trajectories doubly asymptotic to an equilibrium state of saddle type" Mat. USSR Sb. , 6 (1968) pp. 427–437 (In Russian) |
| [a12] | L.P. Shil'nikov, "On a new type of bifurcation of multidimensional dynamical systems" Soviet Math. Dokl. , 10 (1969) pp. 1368–1371 (In Russian) |
| [a13] | L.P. Shil'nikov, "A contribution to the problem of the structure of an extended neighborhood of a rough equilibrium state of saddle-focus type" Mat. USSR Sb. , 10 (1970) pp. 91–102 (In Russian) |
| [a14] | S. Smale, "Differentiable dynamical systems" Bull. Amer. Math. Soc. , 73 (1967) pp. 747–817 |
| [a15] | S. Wiggins, "Global bifurcations and chaos" , Springer (1988) |
| [a16] | S. Wiggins, "Introduction to applied non-linear dynamical systems and chaos" , Springer (1990) |
Homoclinic bifurcations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homoclinic_bifurcations&oldid=18200