Hilbert invariant integral

A curvilinear integral over a closed differential form which is the derivative of the action of a functional of variational calculus. For the functional

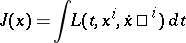it is necessary to find a vector function 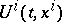, known as a field, such that the integral

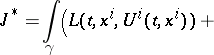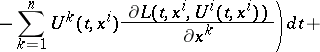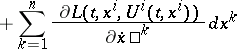is independent of the path of integration. If such a function exists, 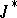is said to be a Hilbert invariant integral. The condition of closure of the differential form in the integrand generates a system of partial differential equations of the first order.

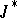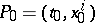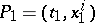The Hilbert invariant integral is the most natural connection between the theory of Weierstrass and the theory of Hamilton–Jacobi. Since is invariant, the value of the Hilbert invariant integral on the curves joining the points and becomes a function of this pair of points, called the action. A level line 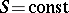is said to be a transversal of 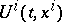. The solutions of 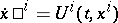are the extremals of 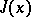. Conversely, if a domain is covered by a field of extremals, the integral 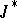constructed from the function 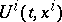, which is equal to the derivative of the extremal passing through 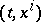, is a Hilbert invariant integral. The possibility of an appropriate contour i.e. of constructing the Hilbert invariant integral, is usually formulated as the Jacobi condition.

If the curve 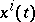passes in a domain covered by a field through the points 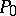and 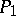, which are also connected by an extremal 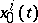, then the invariance of Hilbert's invariant integral and the equality 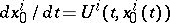yield the Weierstrass formula for the increment of the functional, and hence also a sufficient Weierstrass condition for an extremum (cf. Weierstrass conditions (for a variational extremum)).

For a fixed point 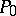the action 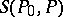is a function 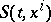of the point 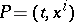, and 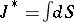. The transition to the canonical coordinates

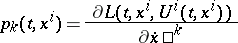makes it possible to write the Hilbert invariant integral as

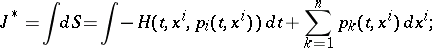where

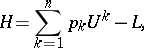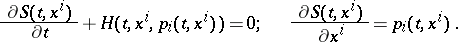These relations are equivalent to the Hamilton–Jacobi equation (cf. Hamilton–Jacobi theory).

The integral 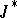for fields of geodesics was introduced by E. Beltrami [1] in 1868, and, for the general case, by D. Hilbert [2], [3], [4] in 1900.

References

[1]	E. Beltrami, Rend. R. Istor. Lombardo Sci. Let. , 1 : 2 (1868) pp. 708–718
[2]	D. Hilbert, "Mathematische Probleme" Nachr. Ges. Wiss. Göttingen (1900) pp. 253–297
[3]	"Hilbert problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German)
[4]	D. Hilbert, "Zur Variationsrechnung" Math. Ann. , 62 (1906) pp. 351–370
[5]	N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian)
[6]	I.M. Gel'fand, S.V. Fomin, "Calculus of variations" , Prentice-Hall (1963) (Translated from Russian)
[7]	C. Carathéodory, "Variationsrechnung und partielle Differentialgleichungen erster Ordnung" , Teubner (1956)
[8]	L. Young, "Lectures on the calculus of variations and optimal control theory" , Saunders (1969)