Heaps and semi-heaps
Algebras with one ternary operation that satisfies certain identities. Heaps are defined by the identities
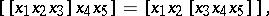 |
 |
while semi-heaps are defined by the identities
 |
All heaps are also semi-heaps.
If, in the set 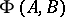 of all one-to-one mappings of a set
of all one-to-one mappings of a set 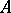 into a set
into a set 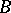 , one defines the ternary operation that puts an ordered triplet of mappings
, one defines the ternary operation that puts an ordered triplet of mappings 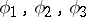 into correspondence with the mapping that is the composite of
into correspondence with the mapping that is the composite of 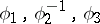 , then
, then 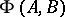 is a heap. Any heap is isomorphic to some heap of one-to-one mappings. If a ternary operation is introduced into an arbitrary group
is a heap. Any heap is isomorphic to some heap of one-to-one mappings. If a ternary operation is introduced into an arbitrary group 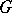 by putting
by putting 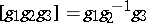 , a heap is obtained (the heap associated with the given group). The concept of a heap was introduced in the study of the above ternary operation on an Abelian group [1]. Heaps have been studied from their abstract aspect [2], [3]. In particular, it was shown by R. Baer [2] that if an arbitrary given element
, a heap is obtained (the heap associated with the given group). The concept of a heap was introduced in the study of the above ternary operation on an Abelian group [1]. Heaps have been studied from their abstract aspect [2], [3]. In particular, it was shown by R. Baer [2] that if an arbitrary given element 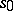 is fixed in a heap
is fixed in a heap 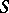 , then the operations defined by the equations
, then the operations defined by the equations 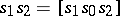 ,
, 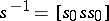 define a group structure on
define a group structure on 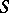 in which
in which 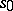 is the unit; the heap associated with this group coincides with the initial heap, while the groups obtained from a heap by fixing various elements of it are isomorphic. In other words, the variety of all heaps is equivalent to the variety of all groups.
is the unit; the heap associated with this group coincides with the initial heap, while the groups obtained from a heap by fixing various elements of it are isomorphic. In other words, the variety of all heaps is equivalent to the variety of all groups.
The set 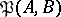 of all binary relations (cf. Binary relation) between the elements of two sets
of all binary relations (cf. Binary relation) between the elements of two sets 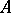 and
and 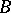 is a semi-heap with respect to the triple multiplication
is a semi-heap with respect to the triple multiplication 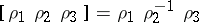 . The set of all invertible partial mappings of
. The set of all invertible partial mappings of 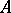 into
into 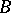 is also closed with respect to the triple multiplication and is a generalized heap [4], i.e. a semi-heap with the identities
is also closed with respect to the triple multiplication and is a generalized heap [4], i.e. a semi-heap with the identities
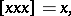 |
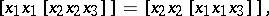 |
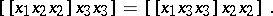 |
Generalized heaps find application in the foundations of differential geometry in the study of coordinate atlases [5]. Heaps are closely connected with semi-groups with involution. If an involution 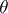 , which is an anti-automorphism, is defined on a semi-group
, which is an anti-automorphism, is defined on a semi-group 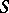 , then the ternary operation
, then the ternary operation 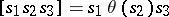 converts
converts 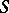 into a semi-heap. Any semi-heap is isomorphic to a sub-semi-heap of a semi-group with involution, [4].
into a semi-heap. Any semi-heap is isomorphic to a sub-semi-heap of a semi-group with involution, [4].
References
| [1] | H. Prüfer, "Theorie der Abelschen Gruppen" Math. Z. , 20 (1924) pp. 165–187 |
| [2] | R. Baer, "Zur Einführung des Scharbegriffs" J. Reine Angew. Math. , 160 (1929) pp. 199–207 |
| [3] | J. Certaine, "The ternary operation  of a group" Bull. Amer. Math. Soc. , 49 (1943) pp. 869–877 of a group" Bull. Amer. Math. Soc. , 49 (1943) pp. 869–877 |
| [4] | V.V. Vagner, "The theory of generalized heaps and of generalized groups" Mat. Sb. , 32 : 3 (1953) pp. 545–632 (In Russian) |
| [5] | V.V. Vagner, "Foundations of differential geometry and contemporary algebra" , Proc. 4-th All-Union. Mat. Conf. , 1 , Leningrad (1963) pp. 17–29 (In Russian) |
| [6] | M. Flato, "Deformation view of physical theories" Czechoslovak J. Phys. , B32 (1982) pp. 472–475 |
Heaps and semi-heaps. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Heaps_and_semi-heaps&oldid=13359