Hardy-Littlewood problem
The problem of finding an asymptotic formula for the number 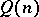 of solutions of the equation
of solutions of the equation
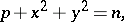 | (1) |
where 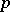 is a prime number,
is a prime number,  and
and 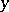 are integers, and
are integers, and  is a natural number
is a natural number 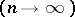 . An analogue of this problem is that of finding the asymptotic behaviour for the number of solutions of the equation
. An analogue of this problem is that of finding the asymptotic behaviour for the number of solutions of the equation
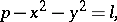 | (2) |
where 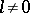 is a fixed integer, and
is a fixed integer, and 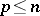 (
(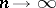 ).
).
The problem was raised by G.H. Hardy and J.E. Littlewood in 1923 and treated by them on the basis of heuristic and hypothetical arguments.
The dispersion method worked out by Yu.V. Linnik enabled him to find an asymptotic expansion for (1):
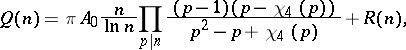 |
where
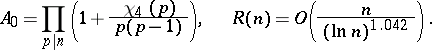 |
From a similar formula for (2) it follows that the set of prime numbers of the form 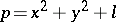 is infinite. By means of the dispersion method an asymptotic expansion has also been found for the number of solutions of the generalized Hardy–Littlewood equation
is infinite. By means of the dispersion method an asymptotic expansion has also been found for the number of solutions of the generalized Hardy–Littlewood equation 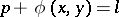 , where
, where 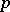 is a prime number and
is a prime number and 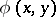 is a given primitive positive-definite quadratic form.
is a given primitive positive-definite quadratic form.
The discussion of the similar equation 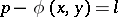 leads to a proof that the set of prime numbers of the form
leads to a proof that the set of prime numbers of the form 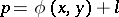 is infinite.
is infinite.
The Vinogradov–Bombieri theorem on the average distribution of prime numbers in arithmetic progressions also gives a solution of the Hardy–Littlewood problem, by replacing the extended Riemann hypothesis by theorems of the type of the large sieve.
References
| [1] | Yu.V. Linnik, "The dispersion method in binary additive problems" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [2] | B.M. Bredikhin, Yu.V. Linnik, "Asymptotic behaviour and ergodic properties of solutions of the generalized Hardy–Littlewood equation" Mat. Sb. , 71 : 2 (1966) pp. 145–161 (In Russian) |
| [3] | B.M. Bredikhin, "The dispersion method and definite binary additive problems" Russian Math. Surveys , 20 : 2 (1965) pp. 85–125 Uspekhi Mat. Nauk , 20 : 2 (1965) pp. 89–130 |
Comments
Of course, this is just one of the many problems raised by Hardy and Littlewood.
Hardy-Littlewood problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy-Littlewood_problem&oldid=13221