Genus of an element of an arithmetic group

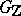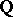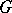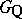The set of elements of the group of units of a connected algebraic -group that are conjugate to a given element in the groups and 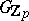for all primes 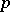, where 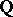and are the field of rational numbers and the ring of -adic integers, respectively. The class of the element is defined as its conjugacy class in 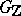. The number of disjoint classes into which the genus of an element decomposes is finite [1], is denoted by 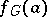, and is called the number of classes in the genus of the element . 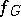The function on arising here is an important arithmetic characteristic expressing the deviation from the local-global principle in questions of conjugacy. In general, 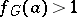. Moreover, if the group is semi-simple and the group 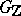is infinite, then 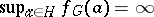for any arithmetic subgroup 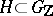(see [1], [3]). The notions considered are a natural modification of the corresponding classical concepts in the theory of quadratic forms and are used in studies of residual approximability of arithmetic groups relative to conjugacy (see [2]).

References

[1]	V.P. Platonov, "On the genus problem in arithmetic subgroups" Soviet Math. Dokl. , 12 : 5 (1971) pp. 1503–1507 Dokl. Akad. Nauk SSSR , 200 : 4 (1971) pp. 793–796
[2]	V.P. Platonov, G.V. Matveev, "Abelian groups and the finite approximability of linear groups with respect to conjugacy" Dokl. Akad. Nauk Bel.SSR , 14 : 9 (1970) pp. 777–779 (In Russian)
[3]	A.S. Rapinchuk, "Platonov's conjecture on the genus in arithmetic groups" Dokl. Akad. Nauk Bel.SSR , 25 : 2 (1981) pp. 101–104; 187 (In Russian) (English summary)