Flat norm
of an  -dimensional polyhedral chain
-dimensional polyhedral chain 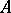 in the space
in the space 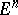
The norm 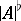 which is defined as follows:
which is defined as follows:
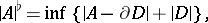 |
where 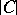 is the mass of the chain
is the mass of the chain 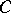 (cf. Mass and co-mass),
(cf. Mass and co-mass), 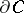 is its boundary, and the infimum is taken over all
is its boundary, and the infimum is taken over all 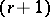 -dimensional polyhedral chains. The properties of the flat norm are
-dimensional polyhedral chains. The properties of the flat norm are
 |
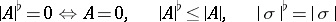 |
for any cell 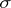 ; if
; if 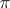 is the projection of
is the projection of 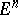 on some plane, one has
on some plane, one has 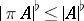 .
.
The completion of the linear space of polyhedral chains 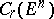 is a separable Banach space,
is a separable Banach space, 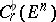 ; its elements are known as
; its elements are known as  -dimensional flat chains, to each of which an infinite or a finite mass can be assigned:
-dimensional flat chains, to each of which an infinite or a finite mass can be assigned: 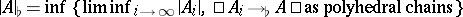 .
.
The boundary 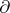 of a flat chain is also defined by passing to the limit; it is a continuous operation, and
of a flat chain is also defined by passing to the limit; it is a continuous operation, and
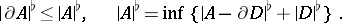 |
The flat norm is the largest of the semi-norms  on
on 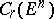 in which all cells
in which all cells 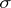 satisfy the inequalities:
satisfy the inequalities: 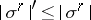 ,
, 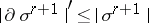 . An
. An  -dimensional flat cochain
-dimensional flat cochain 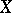 is a linear function of
is a linear function of  -dimensional flat chains
-dimensional flat chains 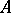 (denoted by
(denoted by 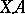 ) such that, for a given
) such that, for a given 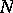 ,
,
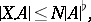 |
where 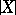 is the co-mass of
is the co-mass of 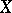 . It is an element of the non-separable space
. It is an element of the non-separable space 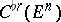 dual to
dual to 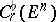 . The flat norm
. The flat norm 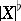 of a flat cochain
of a flat cochain 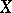 is defined in the standard manner:
is defined in the standard manner:
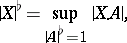 |
so that
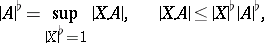 |
and
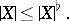 |
For the co-boundary  of a flat chain (defined by the condition
of a flat chain (defined by the condition  ) one has:
) one has:
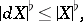 |
so that
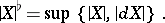 |
Similar concepts are introduced for polyhedral  -dimensional chains situated in open subsets
-dimensional chains situated in open subsets 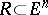 . See also Flat form.
. See also Flat form.
References
| [1] | H. Whitney, "Geometric integration theory" , Princeton Univ. Press (1957) |
Flat norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flat_norm&oldid=12196