Chebyshev method
A method for obtaining a class of iteration algorithms (cf. Iteration algorithm) for finding a simple real root of an equation
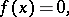 | (1) |
where 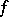 is a sufficiently smooth function.
is a sufficiently smooth function.
The basis of the method lies in the formal representation of the inverse function 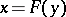 of
of 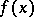 via the Taylor formula. If
via the Taylor formula. If 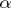 is a sufficiently close approximation to a root of equation (1), if
is a sufficiently close approximation to a root of equation (1), if 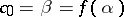 and if
and if 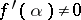 , then
, then
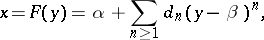 | (2) |
where the coefficients 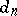 are defined recursively from the identity
are defined recursively from the identity 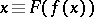 using the Taylor coefficients
using the Taylor coefficients 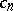 of the function
of the function 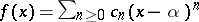 . Putting
. Putting 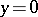 in (2), one obtains the relation
in (2), one obtains the relation
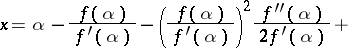 | (3) |
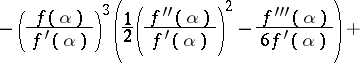 |
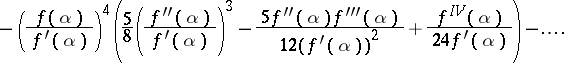 |
Taking a certain number of terms on the right-hand side of (3) gives a formula for the iteration algorithm; with two terms, for example, one obtains Newton's method, while with three terms one obtains an iteration method of the form
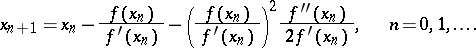 | (4) |
The rate of convergence of the 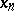 to
to  increases with the number of terms of (3) taken into consideration (cf. [2]). The method can be extended to functional equations (cf. [3]).
increases with the number of terms of (3) taken into consideration (cf. [2]). The method can be extended to functional equations (cf. [3]).
References
| [1a] | P.L. Chebyshev, , Collected works , 5 , Moscow-Leningrad (1951) pp. 7–25 (In Russian) |
| [1b] | P.L. Chebyshev, , Collected works , 5 , Moscow-Leningrad (1951) pp. 173–176 (In Russian) |
| [2] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [3] | M.I. Nechepurenko, Uspekhi Mat. Nauk , 9 : 2 (1954) pp. 163–170 |
Comments
This method is also called Chebyshev's root-finding method. A related approach is based on inverse interpolation, cf. [a1].
References
| [a1] | A. Ralston, "A first course in numerical analysis" , McGraw-Hill (1965) |
| [a2] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a3] | F.B. Hildebrand, "Introduction to numerical analysis" , McGraw-Hill (1974) |
Chebyshev method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_method&oldid=11619