Best complete approximation

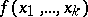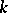A best approximation of a function in variables by algebraic or trigonometric polynomials. Let 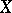be the space 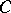or 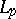of functions , 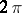-periodic in each variable, that are either continuous or 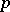-summable () on the 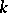-dimensional period cube with edges of length .

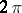The best complete approximation of a function 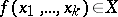by trigonometric polynomials is the quantity

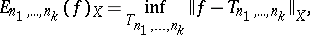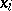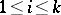where the infimum is taken over all trigonometric polynomials of degree in the variable (). Together with the best complete approximation, one also considers best partial approximations.

A best partial approximation of a function 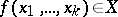is a best approximation by functions 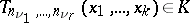that are trigonometric polynomials of degree 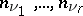(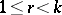), respectively, in the fixed variables 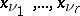with coefficients depending on the remaining 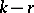variables, i.e.

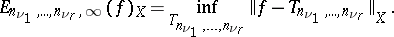It is obvious that

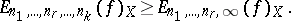S.N. Bernstein [S.N. Bernshtein] [1] proved the following inequality for continuous functions in two variables:

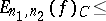(1)

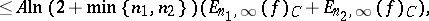where 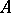is an absolute constant. It has been shown [3] that the term 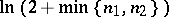in inequality (1) (and in the analogous relation for the space 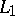) cannot be replaced by a factor with a slower rate of increase as .

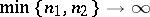In the space 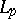(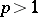) one has the inequality

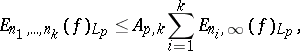(2)

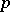where the constant depends only on and .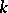

Similar definitions yield best complete approximations and best partial approximations of functions defined on a closed bounded domain by algebraic polynomials, and in this case inequalities similar to (1) and (2) have been established.

References

[1]	S.N. Bernshtein, "Collected works" , 2 , Moscow (1954) (In Russian)
[2]	A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) (Translated from Russian)
[3]	V.N. Temlyakov, "On best approximations of functions in two variables" Dokl. Akad. Nauk SSSR , 223 : 5 (1975) pp. 1079–1082 (In Russian)

References

[a1]	G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966)